One of the most widely used methods to solve a quadratic equation is the quadratic formula. In this blog post, we’ll dive deep into how to use the quadratic formula steps, common mistakes to avoid, and step-by-step examples to help you become a pro at solving these types of equations.
First Things First
Related Blog Posts:
- Quadratic Formula Derivation
- Quadratic Formula Discriminant
- Complete the Square Examples
- How to Teach the Quadratic Formula
Did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? If you’re a student, click here. If you’re a teacher, click here.
Also my How To Teach the Quadratic Formula post here.
This topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
And by the way, if it’s easier for you as a more visual learner, check out my YouTube video where I teach this lesson with the full example below step-by-step.
I also visually show how to plug in the discriminant (in the quadratic formula) into the ti-84 graphing calculator and show common mistakes in the video.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation where the highest exponent (called the degree) of the variable is 2. If the highest exponent is not 2, then don’t even try to use the quadratic formula. It would be wrong 😁
The standard (general) form of a quadratic equation is:
$a x^2 + b x + c = 0$
where a, b, and c are real numbers, and a can’t be zero (otherwise the equation becomes linear). In a nutshell simply put, real numbers are all the numbers on the number line that you can think of.
Quadratic equations can be solved using many methods, such as factoring, Completing the Square, and the quadratic formula. If you want to know how to solve quadratic equations by factoring, check out my step-by-step Youtube video here.
Or, click this link here to watch my video on solving using the Completing the Square method.
The Quadratic Formula to Solve Quadratic Equations in Standard Form
The quadratic formula is a powerful tool for solving any quadratic equation, regardless of the values of a, b, and c. The thing is though that it must be in standard form first to identify those coefficients. Don’t forget to lose sight of our destination: The whole point of the solution after using the quadratic formula is to identify the roots of quadratic functions (in other words, the x-intercepts). The formula is:
$x = \frac{{-b \pm \sqrt{{b^2 – 4ac}}}}{{2a}}$
If you have a hard time remembering this formula, there’s a famous “Pop Goes the Weasel” song that can help you remember. Click here to listen.
If you feel a sense of doom that you even have to memorize this… well, to make you feel better, here is how the quadratic formula is derived.
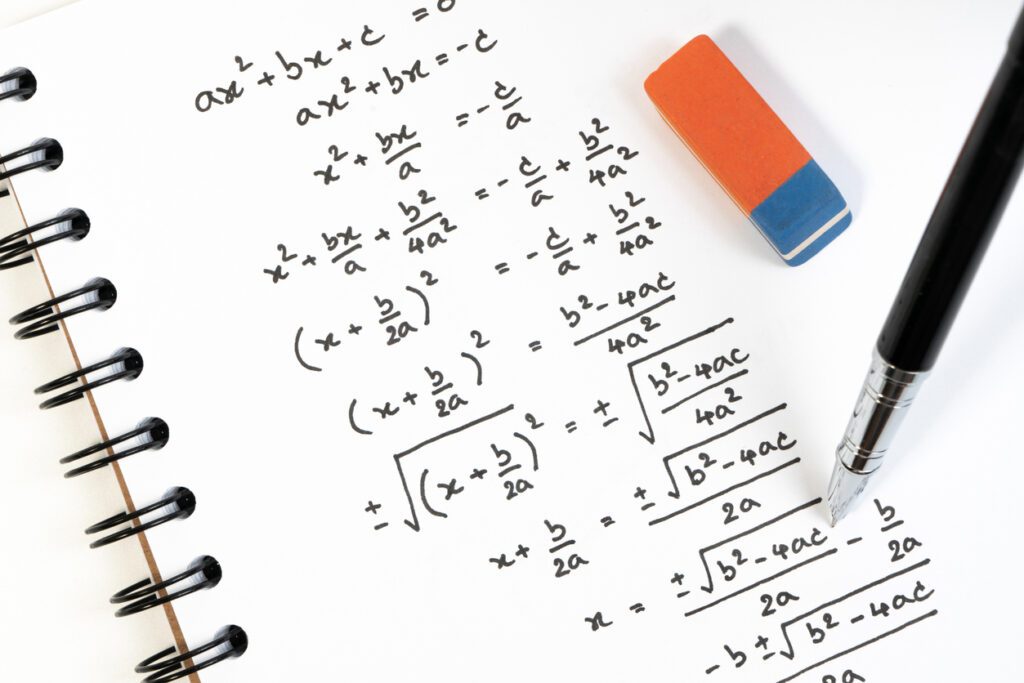
Memorizing doesn’t seem so bad now, huh?
Vocabulary: The discriminant is simply the number underneath the radical (a.k.a. square root). Its formula is therefore $b^2 – 4ac$.
To use the quadratic formula, you first before anything else need to identify the values of a, b, and c in the given quadratic equation, and then plug them into the formula. In a nutshell: a is the coefficient of the $x^2$ term; b is the coefficient of the middle term x; and c is called the constant, in which there is no x attached to it.
The formula can produce up to 2 real solutions. Sometimes there are no real solutions at all (in that case they are both imaginary and happens when the discriminant is a negative number). Other times there’s only 1 real solution (when the discriminant is zero). And the third option is producing 2 real solutions (a positive discriminant).
And again, not to lose sight of why we’re even doing all of this (which is to graph the function without a calculator), is knowing the fact that if there’s:
- 2 real solutions, then there’s 2 x-intercepts.
- 1 real solution, then there’s 1 x-intercept.
- 0 real solutions, then there’s no x-intercepts.
See a pattern here?
Quadratic Formula Example with Answers
Here we go! Let’s work through an example to demonstrate how to solve a quadratic equation using the quadratic formula.
Consider the quadratic equation:
$4x^2 – 8x + 1 = 0$
To solve this equation using the quadratic formula, we need to identify the values of a, b, and c:
a = 4
b = -8
c = 1
Now, we can plug these values into the quadratic formula:
$x = \frac{{-(-8) \pm \sqrt{{(-8)^2 – 4 \cdot 4 \cdot 1}}}}{{2 \cdot 4}}$ $x = \frac{{8 \pm \sqrt{{64 – 16}}}}{{8}}$ $x = \frac{{8 \pm \sqrt{48}}}{{8}}$
Now you can divide everything by 8 right? Because 8, 8, and 48 all have a GCF (greatest common factor) of 8, right?
WRONG! Don’t fall for the trap!
** First of all, you can only divide a whole number by another whole number. Remember that 48 is inside the radical, and so it is not a whole number.
… Okay … so then in that case we’ll just divide only the 8’s.
Wrong again 😆
** The only time you can simplify is if all 3 whole numbers have something in common.
.. I know… You’re probably wondering if I’m delusional because you only see 2 whole numbers (the 8’s). Where’s the third? That’s where simplifying the radical comes into play!
To simplify the square root, we need to find the largest perfect square that divides 48. In this case, the largest perfect square is 16, so we can rewrite the expression as:
$x = \frac{8 \pm 4\sqrt{3}}{8}$
Hurray! Now 8, 8, and 4 have a GCF of 4. So only those we can divide by 4, and we get the two solutions:
$\frac{2 + \sqrt{3}}{2}$ $\frac{2 – \sqrt{3}}{2}$
Now, if you were originally asked to round, let’s say, to the nearest tenth, then you didn’t have to do all of these extra steps. All you needed to do was simply type in the square-root of 48 into your calculator; which is about 6.9.
So now we have $\frac{8 \pm 6.9}{8}$. What this really means, broken up into 2 parts, is:
$\frac{8 + 6.9}{8}$ OR $\frac{8 – 6.9}{8}$.
So punching those into the calculator separately (simplifying first the numerator, and then dividing by 8 last) are the 2 solutions to the nearest tenth: x = 1.9 and x = 0.1.
Common Mistakes to Avoid to Solve Quadratic Equations
In order to solve quadratic equations using the quadratic formula, you gotta be mindful of some common mistakes that students often make. Let’s go over them to make sure you don’t fall into these traps:
1. Forgetting to make the equation equal to zero
The very first quadratic formula step is not immediately identifying a, b, and c believe it or not. You should first before anything make sure that the equation is set equal to zero. What if it’s not equal to zero? You must make it equal to zero by moving around the terms (with opposite operations of course). Remember, the quadratic formula can only be used in standard form, when the equation is in the form $ax^2 + bx + c = 0$.
2. Incorrectly identifying a, b, and c
It’s crucial to correctly identify the values of a, b, and c in the given quadratic equation. Double-checking your work can help you avoid this mistake. Be careful, some teachers like to be sneaky and rearrange the terms around. For example: $-6x + 7x^2 -1 = 0$. In this case, a=7, b=-6, and c=-1.
3. Forgetting to include the negative sign in front of b
When plugging the value of b into the formula, make sure to include the negative sign if b is negative. Forgetting to do this can lead to incorrect solutions.
4. Not putting everything over 2a. In the quadratic formula $x = \frac{{-b \pm \sqrt{{b^2 – 4ac}}}}{{2a}}$ many people I notice only put the square-root section over 2a. It’s all over 2a.
5. Not simplifying the discriminant ($b^2 – 4ac$)
The discriminant is the whole expression under the square root in the quadratic formula. Simplifying this expression first can make the final solution easier to work with.
6. Incorrectly simplifying the square root in which you will most definitely not solve the quadratic equation correctly.
7. When the discriminant is not a perfect square, you’ll need to simplify the square root. Remember, we are looking for perfect-square factors that “go into” the discriminant. A perfect square is a special number such that, if you take the square-root, it equals a whole number. Some of these beautiful numbers are 1, 4, 9, 16, 25, 36, 49, …

8. When punching in the quadratic formula parts in the ti-84 calculator: If you’re asked to leave your answer in simplest radical form, then do not put the square root symbol in your calculator! In other words, just punch in the discriminant (everything underneath). If you’re asked to round to the nearest tenth, then that’s a different story (you can put the square root symbol).
9. Also when plugging in the discriminant inside the ti-84 calculator, make sure to hit the “minus” sign instead of “negative” sign. I see students doing this all the time, and it gives you a wrong answer because the calculator reads it as multiplying by -1instead of subtraction.
Conclusion
To solve a quadratic equation using the quadratic formula is a powerful tool for solving any quadratic equation, regardless of the values of a, b, and c. Practice is key when it comes to solving quadratic equations. The more examples you work through, the more comfortable you’ll become with the process.
Happy solving!



