Understanding Functions and Relations
In a nutshell, the vertical line test tells us whether the relation is a function. The horizontal line test and one-to-one functions are then connected to each other. How so? Well, the horizontal line test tells us whether the inverse is a function; in that case we know whether the relation is one-to-one if it passes both tests.
A function is a special type of relation where each input value is associated with exactly one output value. Huh? Simply put, if there are no repeated x-values, then it’s a function.
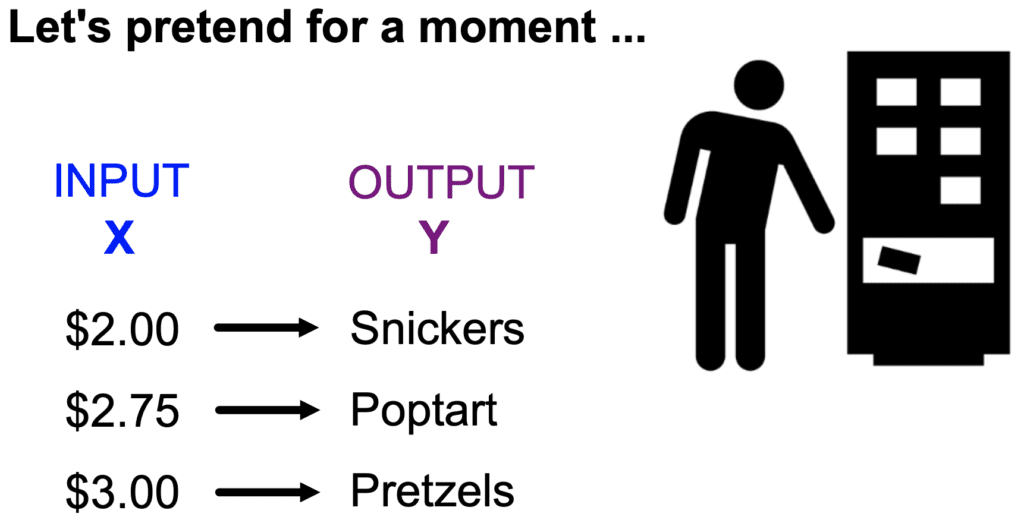
Think of a relation like a vending machine. You input money into the machine (x), and your output is the snack (y). If all of the snacks are different prices (x-values), then the relation is a function because there are no repeating x-values. But let’s say that we can also buy chips for $2.75 as well, then oops! Now the relation is not a function because we can also buy poptarts for $2.75. Get the picture?
Are all relations functions? Is there a test that we can do to quickly determine graphically if a relation is a function? Is the inverse a function? What even is a “one to one” function (also known as 1-1)? Don’t worry, we’ll go over all of it!
This one-to-one correspondence is an important property that distinguishes functions from other types of relations. Determining whether a given graph or equation represents a function is an essential skill for students in Algebra 2 and beyond.
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
You can check out my How To Teach Functions & Relations blog here.
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
And by the way, if it’s easier for you as a more visual learner, check out my YouTube video where I teach this lesson with full examples below step-by-step.
The Vertical Line Test
One of the primary tools used to identify functions is the vertical line test. This test states that if a vertical line hits the graph in more than one spot, then the graph is not a function; plain and simple. Conversely, if a vertical line intersects the graph at exactly one point everywhere, then the graph is a function.
Let’s consider an example. Imagine a graph where a vertical line intersects the graph in multiple points. In this case, the graph would fail the vertical line test, and we can conclude that the relation is not a function. A popular example is a sideways-parabola, which I go over in my YouTube video.
The Horizontal Line Test
While the vertical line test is useful for determining whether a graph represents a function, it doesn’t give us the full picture of the function. To determine if a function is one-to-one, we can use the horizontal line test.
The horizontal line test – plain and simple – tells us whether or not the inverse is a function. And for us to determine if the function is one-to-one, then the graph must pass both vertical and horizontal line tests. The horizontal line test is similar to the vertical line test in that: if the horizontal line intersects the graph at exactly one point everywhere, then we know that the inverse is a function. Conversely, if a horizontal line intersects the graph at more than one point, then the function is not one-to-one.
Passing both the vertical line test and the horizontal line test is required for a function to be one-to-one or 1-1.
Identifying One-to-One Functions
To determine whether a given function is one-to-one, we can follow these steps:
- Apply the vertical line test to the graph of the function. If the graph fails the vertical line test, then the function is not a function, and it is not one-to-one.
- If the graph passes the vertical line test, then the relation is a function. Next, apply the horizontal line test to the graph. If the graph passes the horizontal line test, then the function is one-to-one.
- If the graph fails the horizontal line test, then the function is not one-to-one, even though it might pass the vertical line test.
You Try
Which one below is a one-to-one function?
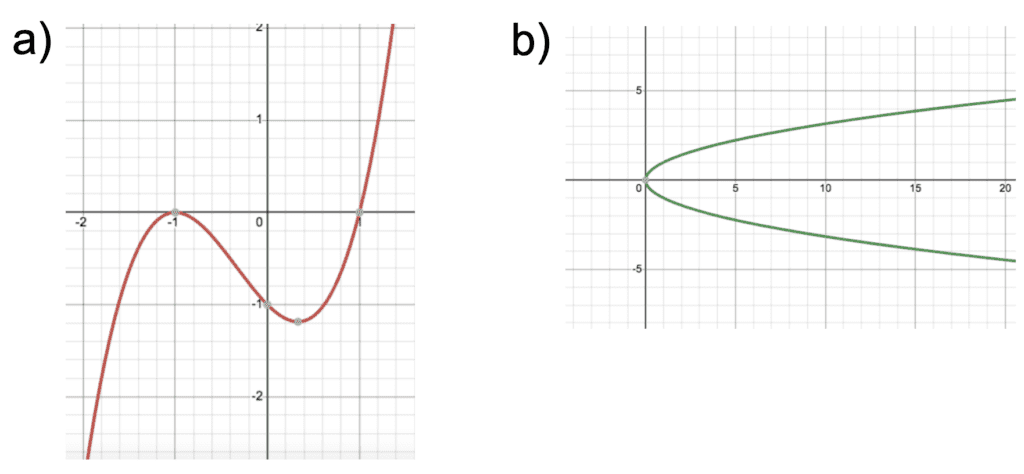
Good job! NEITHER!
In part A, the relation is a function (passes the vertical line test), but the inverse is not a function because it fails the horizontal line test. Remember, to be 1-1 it must pass both tests.
In Part B, the relation is not a function because it fails the vertical line test. The inverse is a function though since it passes the horizontal line test. Buttttt it’s not good enough to be one-to-one.
Practical Applications of One-to-One Functions
One-to-one functions have many practical applications in various fields, including:
- Science and Engineering: One-to-one functions are used to model and analyze relationships between variables in scientific and engineering problems, such as the relationship between temperature and volume in thermodynamics or the relationship between voltage and current in electrical circuits.
- Economics: One-to-one functions are used to model supply and demand curves, where the quantity supplied or demanded is a function of the price of a good or service.
- Finance: One-to-one functions are used to model the relationship between the principal, interest rate, and time in financial calculations, such as compound interest and present value.
- Data Analysis: One-to-one functions are used in data analysis to represent the relationship between two variables, which can be used for prediction, optimization, and decision-making.
Conclusion
The vertical line test and the horizontal line test are powerful tools for identifying one-to-one functions. All it takes is knowing how to draw a straight line, and you’re good to go!