In this blog post, we’ll focus on the difference between adding (and subtracting) rational expressions with multiplying and dividing them. Stick around because towards the end of this blog post we’ll go over many examples step-by-step!
Rational expressions are a fundamental concept in algebra, and understanding how to perform operations on them is mandatory for success in higher-level mathematics. If you’ve learned it in a 9th grade algebra class, then you’re ahead of the curve; because operations of rational expressions is extensively used in precalculus and calculus!
We’ll also explore how factoring plays a huge role in this since we’ll be simplifying these rational expressions as much as possible. You can catch my resources on factoring below:
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra FYI!
You can watch my YouTube Video as I go over the operations:
Understanding Rational Expressions
A rational expression is a mathematical expression that can be written as a fraction, with a polynomial in the numerator and a non-zero polynomial in the denominator. If that definition scares you, it’s pretty much just a polynomial over another polynomial; except we can’t have zero at the bottom since it would then be undefined.
If you forgot what a polynomial even is, don’t worry! You can catch my blog post on that here.
And why is a rational expression a fraction? Well, what word do you see in the word “rational”? The word ratio! A ratio can be written in 3 different ways; one of them being a fraction. That’s where the term comes from.
Before we delve into the operations, it’s important to understand the foundational concepts of rational expressions.
Skills You Need To Start Operations of Rational Expressions
Especially when multiplying and dividing rational expressions, factoring is a crucial step in simplifying rational expressions, as it allows you to identify common factors and cancel out terms. In a nutshell, if stuff doesn’t start cancelling out, then you probably factored it wrong. So again, take a look at those resources I wrote down for you at the beginning of this blog post to jog your memory on factoring.
Next, it’s important to be comfortable with the rules of exponents and the properties of fractions, as these will come into play when performing operations on rational expressions.
You need to know that adding and subtracting rational expressions is similar to performing those operations for general fractions: You need to find the LCD (least common denominator) in order to create common denominators.
Similarly, the same skills for multiplying and dividing fractions will be used to multiply and divide rational expressions. Remember that when we multiply fractions, you multiply “straight across”. In other words, top times top, and bottom times bottom.
And then for dividing fractions we’ll end up doing the good ol’ keep, change, flip.
Addition and Subtraction of Fractions
When adding or subtracting fractions, you must find a common denominator. And then afterwards, you combine the numerators. A common mistake that I see students make is to also combine the denominators as well. Nope. Keep the common denominator the same in your final answer; only the top changes.
To find the common denominator, you must find the LCD: The least common denominator is the smallest non-zero value that is a multiple of all the denominators in the expression.
For example, the LCD of 3 and 5 is 15. We simply multiply 3 and 5 together. We do this because 3 times nothing equals 5. And 5 times nothing equals 3.
How about the LCD of 4 and 20? Sure, you can technically multiply 4 and 20 together to get 80 as a common denominator. But 80 is not the least common denominator. This is because we can multiply 4 times 5 to get to 20. And so the LCD is actually 20.
Going back to the number 80 in the previous example, if you want, you can definitely use that as a common denominator; but then what this means is that you’ll have to simplify the fraction later and work with much larger numbers. That’s why the LCD is nice; it saves us time and lets us work with smaller numbers.
Addition and Subtraction of Rational Expressions
Similarly, to add or subtract rational expressions with a common denominator, you simply add or subtract the numerators (combine them) and then keep the common denominator. However, if the denominators are not the same, you must first find the LCD and then rewrite each expression with the LCD as the denominator.
Here’s the step-by-step process for the addition and subtraction of rational expressions:
- Identify the LCD of all the denominators.
- Rewrite each rational expression with the LCD as the denominator.
- Add or subtract the numerators, keeping the LCD as the denominator.
- Simplify the resulting expression by factoring and canceling common factors, if possible.
Example:
Let’s look at an adding example: $ \frac{5x^2}{2x + 2} + \frac{3x + 1}{x + 1} $. The very first thing I tell my students to do is to put parenthesis around the numerator or denominator that has more than one term. It looks like this: $ \frac{5x^2}{(2x + 2)} + \frac{(3x + 1)}{(x + 1)} $. This reminds our brain that these are binomials that we are working with.
To add these expressions, we first need to find the least common denominator (LCD). Since we can’t multiply (2x+2) times anything to get to (x+1), and vice versa, then in this case the LCD is them multiplied together: (2x + 2)(x + 1).
Next, we rewrite each expression with the LCD as the denominator. We can accomplish this by multiplying each fraction (top and bottom of course) by the denominator of the other: $ \frac{(5x^2)(x + 1)}{(2x + 2)(x + 1)} + \frac{(3x + 1)(2x + 2)}{(x+1)(2x + 2)} $. Remember that because of the commutative property of multiplication, $ (x+1)(2x + 2) $ is the same thing as $ (2x+2)(x+1) $. And so we do, in fact, have common denominators.
Now that we have common denominators, we can combine (in this case add) the numerators. Make sure to always keep the LCD as the denominator: $ \frac{5x^2(x+1) + (3x+1)(2x+2)}{(2x + 2)(x + 1)} $
Now we have to simplify the numerator by using PEMDAS. In other words, first we use the distributive property, and then add last. After multiplying, we have: $ \frac{(5x^3 + 5x^2) + (6x^2 + 6x + 2x + 2)}{(2x + 2)(x + 1)} $
Now combining like-terms we have: $ \frac{5x^3 + 11x^2 + 8x + 2}{(2x + 2)(x + 1)} $
And we are done! If you want, you can totally distribute the denominator, but it is not necessary.
Multiplication of Rational Expressions
Remember that adding rational expressions (and subtracting) we must have a common denominator. But multiplying and dividing rational expressions, we do not need a common denominator.
Multiplying rational expressions is a straightforward process, as you do not need to find a common denominator.
After factoring each polynomial (if factorable), keep in mind that an easier way to simplify is to cross out common factors diagonally. Again, take a look at my YouTube Video for an example of this. See the screenshot of my multiplication example below:

When multiplying rational expressions, it’s important to remember that the order of the factors does not matter, as multiplication is commutative. This means that you can rearrange the factors in any order without changing the final result.
And again if you forgot how to factor, you can watch my factoring YouTube video lesson here.
Division of Rational Expressions
Dividing rational expressions is similar to multiplying them, but with a slight twist. To divide one rational expression by another, you can rewrite the division as a multiplication problem by taking the reciprocal of the divisor and then multiplying.
People know this as keep, change, flip!
The steps for dividing rational expressions are as follows:
- Keep the left fraction.
- Change the division symbol to a multiplication symbol.
- Flip (find the reciprocal) the second fraction.
- To multiply fractions, remember you multiply straight across.
- Simplify the resulting expression by factoring and canceling common factors, if possible.
It’s important to note that when dividing rational expressions, the order of the factors does matter, since division is not commutative. This means that you cannot simply swap the numerator and denominator of the divisor and expect the same result.
See screenshot of my YouTube Video below where I show a division example:
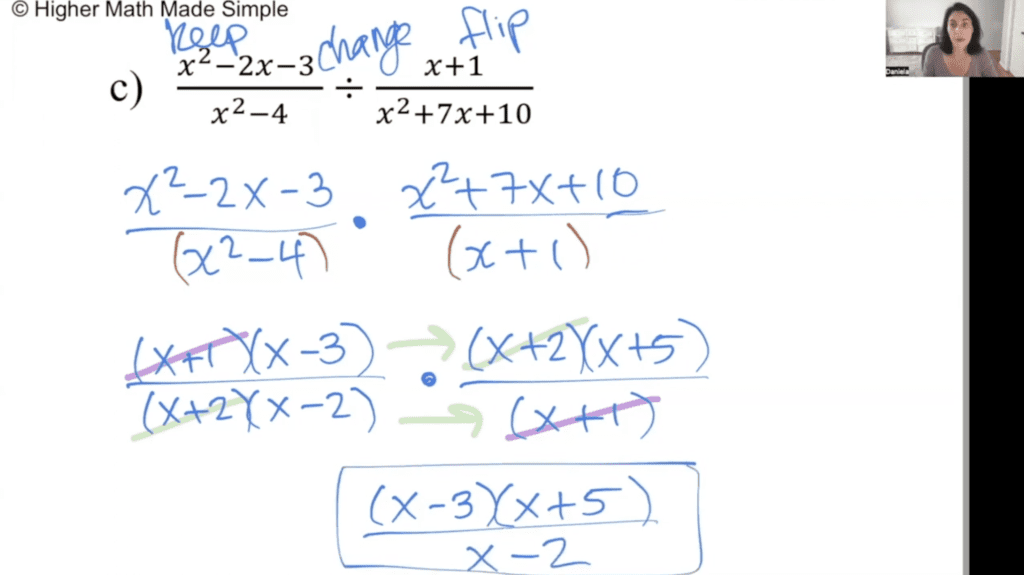
In some cases, you may need to use long division to divide rational expressions, especially when the degree (highest exponent) of the top is greater than the degree of the bottom.
Again, you can watch my YouTube Video as I go over a long division example step-by-step. See screenshot below:

Simplifying Rational Expressions
After performing the various operations on rational expressions, it’s often necessary to simplify the resulting expression. Simplifying involves factoring the numerator and denominator and then canceling out any common factors.
The key steps for simplifying rational expressions are:
- Factor the numerator and denominator, if possible.
- Identify any common factors between the numerator and denominator.
- Cancel out the common factors, reducing the expression to its simplest form.
Simplifying rational expressions is an important skill, as it can make the expression easier to work with and understand.
Practical Applications and Examples
Rational expressions have a wide range of applications in various fields, including physics, engineering, and economics. Understanding how to perform operations on rational expressions can be really useful in the following scenarios:
- Solving Equations: Rational expressions often appear in equations that need to be solved. Mastering the techniques for adding, subtracting, multiplying, and dividing rational expressions can help you solve these equations more efficiently.
- Modeling Real-World Situations: Rational expressions can be used to model various real-world situations, such as rates, ratios, and proportions. Being able to manipulate these expressions can help you solve problems related to these concepts.
- Calculus and Advanced Mathematics: Rational expressions are fundamental to many advanced mathematical concepts, such as limits, derivatives, and integrals. Proficiency in working with rational expressions is vital for success in these higher-level mathematics courses.