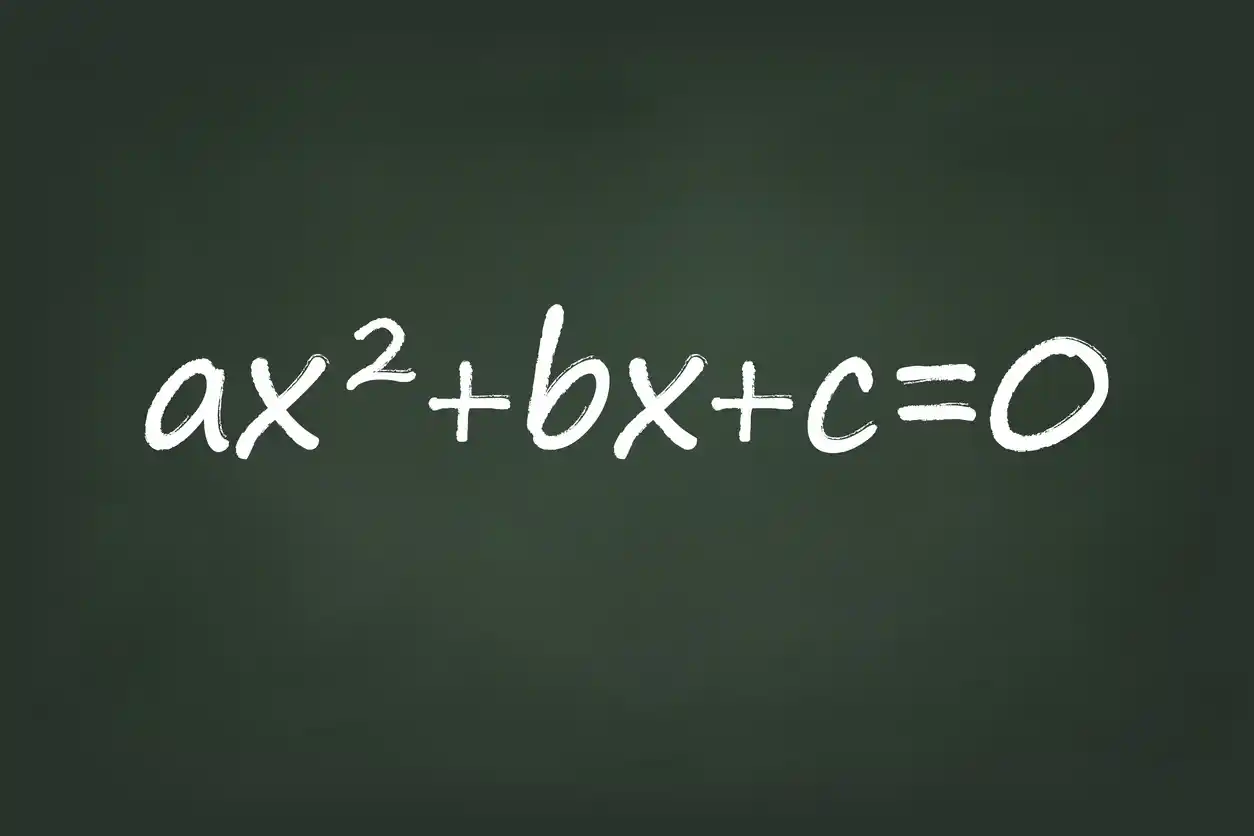What is the AC method? In this blog post we’ll explore step by step using plenty of examples how to factor using the AC method. We’ll also look at a scenario where it’s not factorable.
This method is only used for quadratic trinomials in standard form $ax^2+bx+c$. Quadratic means that the degree (highest exponent) is 2, and trinomial means it has 3 terms. There are two cases that we’ll talk about in depth here: one where the leading coefficient a equals 1, and the other when a is NOT 1.
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
Teachers can also access my lessons, keys, reference sheets for:
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
Connection
In general, there are 3 different ways that we can solve quadratic equations:
If an equation is not factorable (we’ll go over an example of that too later), then you must use either complete the square or quadratic formula to solve for the roots/solutions. Remember that the whole point in solving for the roots is that the real solutions translate to the number of x-intercepts of the parabola.
AC Method: $ax^2 + bx + c $ where $a = 1$
Standard form of a quadratic equation is $ax^2 + bx + c $. What is the AC method? I tell my students that a way to remember the AC factoring method is this statement that rhymes: Factors of $a \times c$ must add up to $ b $.
For example: $x^2 + 11x + 10$. First you should define the a, b, and c values. In this problem, a=1, b=11, and c=10. We must first find the value of $a \cdot c$ which is $1 \cdot 10=10$. Now we must do a factor tree of all the factors; the full list, where the signs matter. So the list of factors are:
- $1 \times 10$
- $-1 \times -10$
- $2 \times 5$
- $-2 \times -5$
Within the rhyming phrase (factors of $a \times c$ must add up to $ b $), we can see that now we must add each set of factors to see which of those add up to b=11.
- $1 \times 10$ $\rightarrow$ $1+10=11$
- $-1 \times -10$ $\rightarrow$ $-1+-10=-11$
- $2 \times 5$ $\rightarrow$ $2+5=7$
- $-2 \times -5$ $\rightarrow$ $-2+-5=-7$
So the factors 1 and 10 are the lucky winners!
Now, when you are solving a=1 problems, the beauty is that there is a shortcut method. The template is $(x + \text{something})(x + \text{something})$, where the chosen factors go into those “something” spots. So factored form is $(x+1)(x+10)$. It doesn’t matter which factor you put in first because of the commutative property.
Don’t forget to do a check! If you perform the distributive property (or FOIL), you’ll get the original problem after combining like terms.
AC Method: $ax^2 + bx + c $ where $a \neq 1$
For example: $2x^2 +x -6=0$. Let’s define a=2, b=1, and c=-6. Remember that Factors of $a \times c$ must add up to $ b $.
We must first find the value of $a \cdot c$ which is $2 \cdot -6 = -12$. Now we must do a factor tree of all the factors; the full list, where the signs matter. So the list of factors are:
- $1 \times -12$
- $-1 \times 12$
- $2 \times -6$
- $-2 \times 6$
- $3 \times -4$
- $-3 \times 4$
Within the rhyming phrase (factors of $a \times c$ must add up to $ b $), we can see that now we must add each set of factors to see which of those add up to $b=1$.
- $1 \times -12$ $\rightarrow$ $1+-12=-11$
- $-1 \times 12$ $\rightarrow$ $-1+12=11$
- $2 \times -6$ $\rightarrow$ $2+-6=-4$
- $-2 \times 6$ $\rightarrow$ $-2+6=4$
- $3 \times -4$ $\rightarrow$ $3+-4=-1$
- $-3 \times 4$ $\rightarrow$ $-3+4=1$
So the factors -3 and 4 are the lucky winners!
THE TWIST: Factor By Grouping (4 terms)
Unfortunately in this example $2x^2 +x -6=0$, since a is not equal to 1, we can’t do the shortcut method here. We need to prepare ourselves to use the Factor by Grouping method. If you forgot how to use that method, don’t worry I have a YouTube video about the Factor by Grouping method here.
So what do we do with the chosen factors -3 and 4? Great question.
We’re going to use those chosen factors as coefficients of the x terms, and add them together. In other words, $-3x+4x$ or $4x + -3x$. Either way, these simplify to $x$. I wonder how this helps us …
In $2x^2 +x -6$, notice that $x$ is the exact middle term. That’s not a coincidence. So what we’ll now do is convert this trinomial (3 terms) into 4 terms: $2x^2 -3x+4x-6$. It doesn’t matter which order you write the factors in because of the commutative property of addition.
Why would we go through all this trouble to convert the trinomial into 4 terms? This is where Factor by Grouping comes into play. With this method, you can only attempt it with 4 terms. What we’ll do is split the 4 terms into 2 groups of 2 terms each: $(2x^2 -3x)(+4x-6)$. Note that this is not multiplication; I just like to remind myself that the $4x$ term is positive.
Now we’ll factor each group using the GCF method. The GCF of the first group is $x$, and the GCF of the second group is 2. So we have: $x(2x-3)+2(2x-3)$. If the parenthesis match, then you know you did all the steps correctly.
Now with these 2 final terms, the GCF is the matching parenthesis $(2x-3)$, so we’ll pull that out. What’s then left is the two terms outside the parenthesis: $(x+2)$.
So finally factored form is $(2x-3)(x+2)$.
PS … if you forgot how to factor using the GCF method. Don’t worry, I gotchu! I made a YouTube video on using the GCF method too.
What If It’s Not Factorable?
How do we know if a quadratic trinomial is not factorable? That’s when the AC factor method fails. Let’s take a look at factoring the quadratic expression $3x^2-4x+2$. Let’s define a=3, b=-4, and c=2.
We must first find the value of $a \cdot c$ which is $3 \cdot 2 = 6$. Now we must do a factor tree of all the factors; the full list, where the signs matter. So the list of factors are:
- $1 \times 6$
- $-1 \times -6$
- $2 \times 3$
- $-2 \times -3$
Within the rhyming phrase (factors of $a \times c$ must add up to $ b $), we can see that now we must add each set of factors to see which of those add up to $b=-4$.
- $1 \times 6$ $\rightarrow$ $1+6=7$
- $-1 \times -6$ $\rightarrow$ $-1+-6=-7$
- $2 \times 3$ $\rightarrow$ $2+3=5$
- $-2 \times -3$ $\rightarrow$ $-2+-3=-5$
Nope! None of them add up to -4. So this is not factorable!