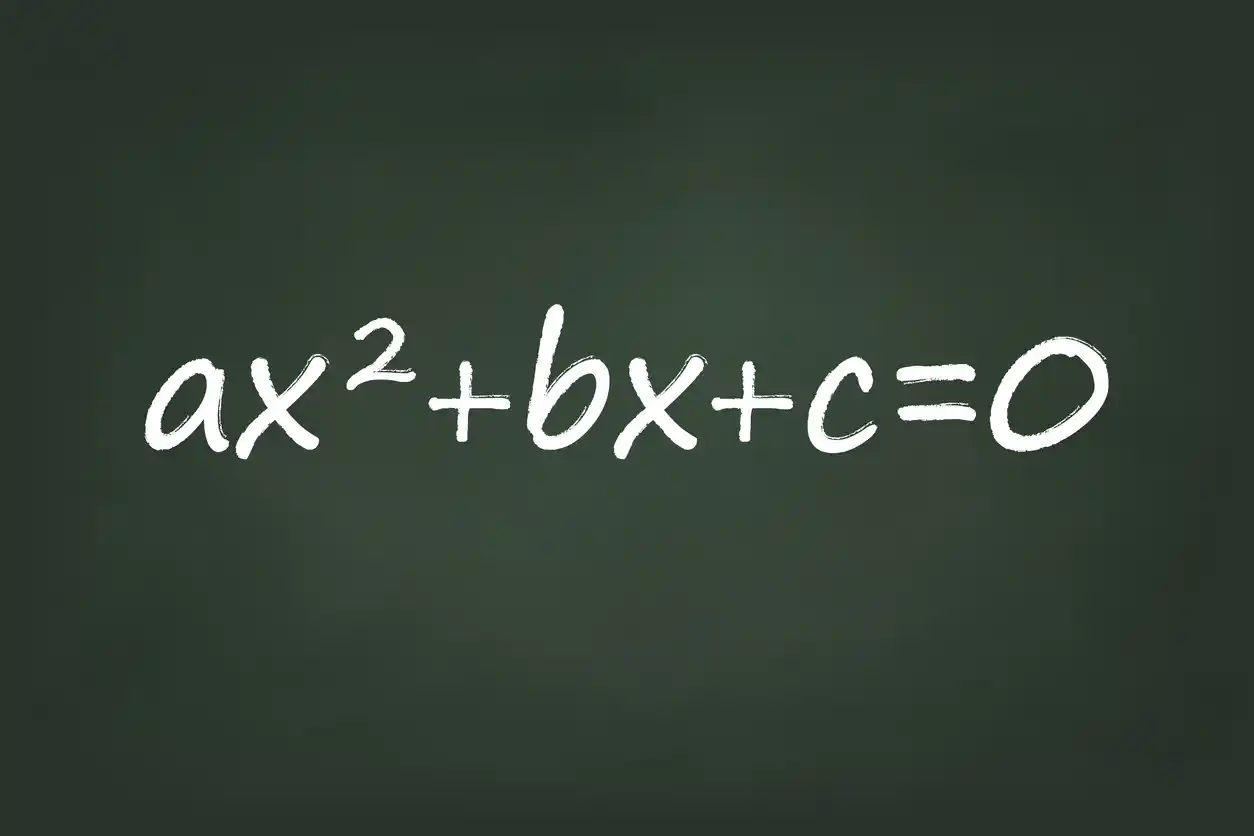Complete the Square Examples

In this blog post, we’ll go over a couple of Complete the Square examples: one from this blog, and the other you can see visually from my YouTube video. As a math student, you’ve come across 3 different ways for solving quadratic equations: factoring, quadratic formula, and then complete the square method. The whole point in these methods is that the roots (solutions) you are solving for are the locations of the x-intercept(s) of the parabola.

If you happen to be a teacher reading this blog post, you can head over to my teacher blog where I talk about the effective methods in teaching the complete the square method.

First Things First

If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.

Also my How To Teach the Complete the Square Method post here.

If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra FYI!

Check out these related blog posts:

• Solve Quadratic Equations Example with a YouTube video about it.
• Quadratic Formula Derivation

Application

Not only is the Complete the Square steps used to solve for the roots of a quadratic equation, but it’s also used to derive the Quadratic Formula. Take a peek at my blog post that goes over the quadratic formula derivation here.

Understanding the Basics of Quadratic Equations

Before we delve into the complete the square method, let’s quickly review the fundamental structure of a quadratic equation. The standard form of a quadratic equation is $ax^2 + bx + c = 0$,

where a, b, and c are real numbers, and a is not equal to 0 (or else it because linear since anything times zero is zero).

The coefficients a, b, and c play a crucial role in determining the nature and solutions of the equation. Specifically:

• a is the coefficient of the $x^2$ term, also known as the leading coefficient.
• b is the coefficient of the x term.
• c is the constant term, which does not have an x attached to it.

Understanding these components will be essential as we dive into these complete the square examples.

The Step-by-Step Process of the Complete the Square Method

The complete the square method is really, believe it or not, a geometric approach to solving quadratic equations. Check out that blog post here where I derive the steps geometrically; it’s pretty cool honestly. I also have a complete the square worksheet (with key) that guides you in deriving the steps.

You can also watch how I derive the Complete the Square steps in my YouTube video:

In the complete the square examples that I show you, one of the steps involves transforming the quadratic equation into a “perfect square trinomial”, which then allows us to finally find the solutions by taking the square-root of both sides. Let’s walk through the step-by-step process:

Step 1: Make Sure the Leading Coefficient “a” is 1

If the leading coefficient a is not equal to 1, then just divide everything by a to make it 1. This ensures that the equation is in the standard form $1x^2 + bx + c = 0$.

Let’s look at a specific example. How about we solve: $2x^2 + 16x + 4 = 0$.

Given a = 2, we need to divide everything by 2. This doesn’t actually change the answers because you’re dividing to every term. And so now we have $1x^2 + 8x + 2 = 0$

Step 2: Move the Constant Term to the Other Side

Next, we need to move the constant term c to the other side of the equation by adding or subtracting it from both sides (whatever is opposite).

In the specific example above, we now have: $1x^2 + 8x = -2$

Step 3: Determine the “Magic Number” to Add on Both Sides

The next key for the complete the square method is to add a very special number to both sides of the equation. I phrase it this way because it’ll turn the expression on the left-hand side to, what’s called, a Perfect Square Trinomial. This simply means that some trinomial (3 terms) $1x^2 + bx + c$ can be factored as the perfect square generally as: $(x + \frac{b}{2})^2$ … but this is actually Step 4 later.

The special number that we’re adding to both sides is calculated by taking half of b, and then squaring it. Simple as that; don’t make it any complicated that it needs to be! This “magic number” is essential for transforming the equation into a perfect square trinomial.

In the example, b = 8. We’ll take half of it; so 4. And then squaring 4 we get 16. So we’ll add 16 to both sides. *Note: As long as you add the same number to both sides of any equation, you’ll never change the answer. How about that!

So now it looks like: $x^2 + 8x + 16 = -2 + 16$

Step 4: Factor and Simplify the Equation

The left side will now be a Perfect Square Trinomial, which needs to be factored (don’t worry there’s a template for that), while the right side will be that magic number plus the original constant term.

To factor the left-hand side, you can if you want factor using the “AC Method” (video on that here), but it’s not necessary. Luckily there’s a template.

I snuck in that template into your subconscious on Step 3; that’s $(x + \frac{b}{2})^2$. So in a nutshell, it’s always “x plus something” squared. That “something” is always half of b. Is this starting to make some sense?

** I do need to say (common mistake) that the special number will always be positive, since anything squared is always positive.

** I also need to say that if b is negative, then it would be “x minus something” squared; since adding a negative is the same thing as minus.

Anyway back to the complete the square example: Given b=8, then half of that is 4. So now we’re at $(x+4)^2$.
And then simplifying the right-hand side, it’s $-2 + 16 = 14$.

So at this stage we have: $(x+4)^2 = 14$

Step 5: Solve Using the Square Root Method

The final step is to solve the equation using the square root method. Why is it called that? Because we’ll take the square-root of both sides. Duh! ** Remember to always include the positive and negative sign ($\pm$), since the square root can create two possible solutions. **

We’re at $x + 4 = \pm \sqrt{14}$. What does this even mean? This means either $x + 4 = \sqrt{14}$ or the other solution is $x + 4 = -\sqrt{14}$.

Now, if in the directions it asks you to round to the nearest tenth, which is $\sqrt{14} = 3.7$, now we have $x + 4 = 3.7$ or $x + 4 = -3.7$. And subtracting 4 on both sides for both equations, our final answers are -0.3 and -7.7.

Now, if the directions ask you to leave it in “simplest radical form”, that means you leave it in the radical. Duh! First make sure that the radical is in simplest form. Is there a perfect square that goes into 14? Nope. So the 2 solutions are $x = \sqrt{14} – 4$ and $x = -\sqrt{14} – 4$.

Reference Sheet

You can find this reference sheet along with my complete the square worksheet (with key) here.