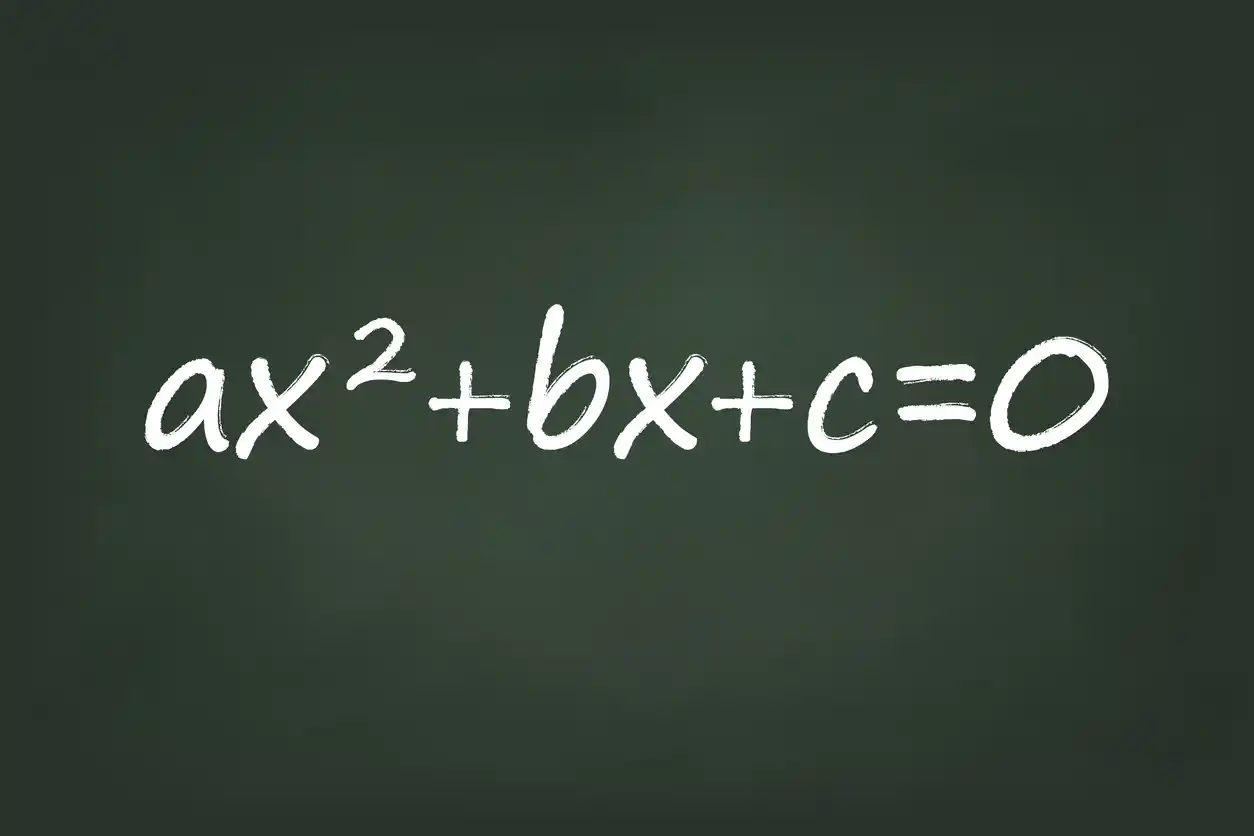I highly suggest before even showing students an example on how to use the complete the square method (to solve a quadratic equation), to first derive the complete the square steps. You can either read that blog post here and/or watch that youtube video here.
That is, only if you have the time in your crazy busy curriculum! But I’ve found that students knowing where it comes from helps them realize that it’s not just a random series of steps. Them realizing that it’s actually a geometric technique is pretty cool. And on top of that, given that they’ve taken geometry (or will take soon), it’s awesome for them to see how math subjects are all connected.
If you enjoyed the scaffolded packet that I used to help students derive the steps shown in the above video/blog, you can access that warm up, activity packet (with keys), and reference sheet here.
Teaching the Complete the Square Method
Okay, now getting into teaching students how to solve using the complete the square method, you can watch how I approach it in my student blog post here. I also made a video about it below:
If you notice just by the thumbnail of my video above, you can see that I write the general steps on the right side, while simultaneously working on an example on the left side for solving a quadratic equation.
This I’ve found has been the best way for students to see the complete the square method in live action. Simply showing the steps or doing an example separately, I find that this makes it more difficult for students to follow along and/or makes it more difficult to make the connections.
You can afterwards give your students the complete the square method reference sheet with corresponding example here.
Another way is to hand out that reference sheet first, and then have students refer to it as you go over the example on the board. But again, given most students are visual learners, just by having those steps written on the board while you pointing to them makes all the difference in the world.
Many times as teachers, given we know the content inside and out, we tend to forget that our students are learning the material for the very first time. And so trying to make it as visual as possible is the best way, especially since students memorizing 5 steps is like we’re asking them to memorize an entire 5-page essay 😂
How to Start
I would recommend starting out with a Warm Up example of a quadratic equation in standard form, and students must identify the a, b, and c values. This will help it make more of a seamless transition when going over the complete the square steps later.
Tell students that there are 3 different ways to solving a quadratic equation in standard form. What are they? Factoring, completing the square, and quadratic formula. This helps students understand first of all what the whole point of completing the square is even for.
Common Mistakes
- A common mistake I see is the step where students square half-of-b. If the b value is negative, then they end up adding a negative number to both sides of the equation. So make sure to emphasize that they should always be adding a positive number since squaring a positive number is always positive.
- Students forget to divide everything by a if it is not equal to 1. So make sure to stress this too!
- I can’t tell you how many times students forget the plus/minus symbol as they use the square-root method to solve for x.
Applications
The first application is that the complete the square method is used to convert a standard form equation into vertex form.
The complete the square steps is also used to derive the Quadratic Formula, which is another method for solving a quadratic equation. The quadratic formula is really the complete the square method done for you!
You can watch my video on the derivation of the quadratic formula using the complete the square method. I also made a blog post on that here. And I made a scaffolded worksheet (with warm up and key) where students are guided to derive the quadratic formula.
If you’re interested in seeing how I teach the quadratic formula, check out that blog post here, or that video here.
Complete the Square Steps
- Start with the standard form of the quadratic equation: $ax^2 + bx + c=0$
- Make the leading coefficient a equal to 1 by dividing the entire equation by a.
- Move the constant term c to the other side of the equation
- Take half of the coefficient of the x term (b), square it, and add it to both sides of the equation
- The resulting equation will be a perfect square trinomial, in which you use the template $(x + \frac{b}{2})^2$ to get it into factored form.
- Finally, we can solve for x by using the Square-Root Method (taking the square root of both sides).
You can also grab my reference sheet along with warm up, activity packet (with keys), and reference sheet here: