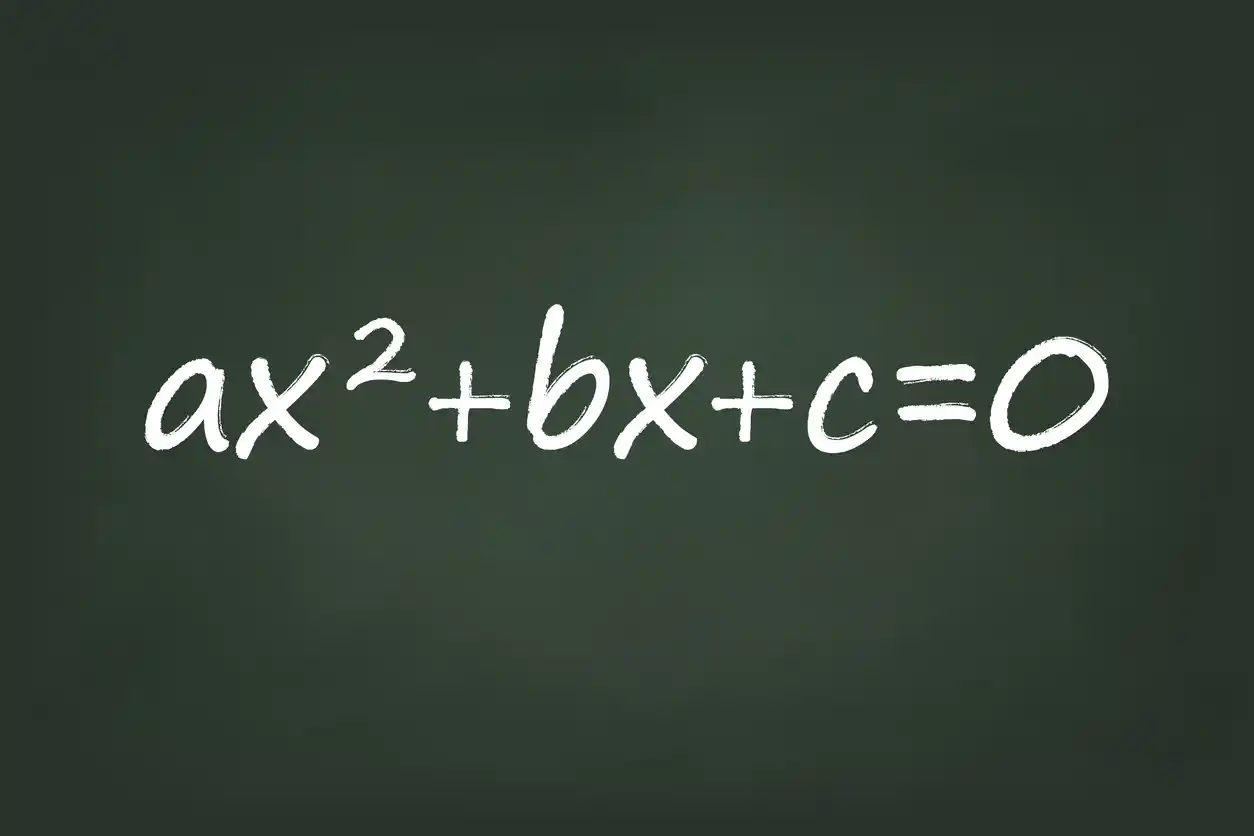Deriving Complete the Square Steps

In this blog post, we’ll be deriving Complete the Square steps as a geometrical representation. Completing the square is a powerful algebraic technique that allows us to solve quadratic equations and derive the quadratic formula (you can read that blog post here). This method involves visualizing and manipulating squares and rectangles to transform a quadratic expression into a perfect square trinomial. We’ll dive deep into the derivation of the complete the square steps, exploring cool concepts and making important connections that will absolutely deepen your understanding of this essential algebraic tool.

If you’re a teacher reading this blog post, feel free to head over to my teacher blog where I show effective methods in teaching complete the square method to students.

I also have a deriving the complete the square scaffolded packet with reference sheet here.

First Things First

If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.

Also my How To Teach the Completing the Square Method here.

If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra FYI!

Grab the packet with keys and reference sheet that I use to go over this blog post as well as my complete the square youtube video below!

Laying the Groundwork

Before we delve into deriving the complete the square steps, it’s super important that we learn to walk before we run. We need to go over some key concepts as a Warm Up that is directly related to deriving the complete the square method.

Adding the Same Number to Both Sides

One of the steps in the complete the square formula is to add the same number to both sides of an equation. This is perfectly fine since it does not change the solution.

Don’t believe me? Let’s take a look at the example $2x – 3 = 9$. Adding 3 to both sides then dividing by 2, the solution is $x = 6$.

Now, pick a number. Any number! Doesn’t matter how big or small. How about 7? Let’s add 7 to both sides: $2x – 3 + 7 = 9 + 7$. Combining like-terms (the whole numbers) on both sides of the equation, we get a “new” equation: $2x + 4 = 16$. Then subtracting 4 on both sides and dividing by 2 … surprise, surprise! We get the same answer.

Point made. The thing is though, that we won’t just be adding any number, but a very special and magic number; one that creates a Perfect Square Trinomial. Don’t worry, we’ll talk about that later.

Visualizing Squares and Rectangles

The complete the square method is a visual geometric procedure, as it involves the manipulation of squares and rectangles.

Let’s introduce the idea of a square with an area of $x^2$. The formula is $\text{side}^2$, and remember that all sides are equal.

We’ll also look at a a rectangle with an area of $6x$, where the formula is $\text{length} \times \text{width}$. Remember also that opposite sides have equal length.

Deriving the Complete the Square Steps

Now that we have a solid foundation in place, let’s dive into the step-by-step derivation of the complete the square method.

Step 1: Start with a Square of Area $x^2$.

Step 2: Add a Rectangle with Area $6x$.

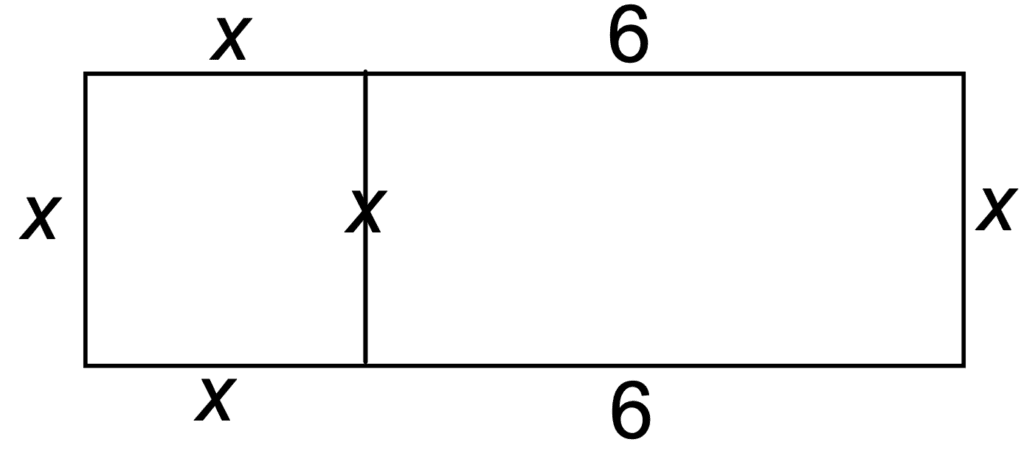
Remember that opposite sides have equal length. And that the area of a rectangle is $\text{length} \times \text{width}$, whereas the area of a square is $\text{side}^2$.

Step 3: Express the Total Area of the Large Rectangle.

Now we have a large rectangle, where the width is x and the length is $x + 6$. Then the total area is $x(x+6)$, which using the distributive property we get the more simplified version: $x^2 + 6x$.

Step 4: Cut the 6x Rectangle in Half (Divide by 2).

What is $\frac{6x}{2}$? This creates two rectangles with an area of 3x each.

Step 5: Erase the 6x Rectangle, and Add the Two 3x Rectangles.

The two 3x rectangles are added to the right side of the square and below the square.

The total area is still $x^2 + 6x$ because all we did was move the “puzzle pieces” around.

Now we end up with a missing piece.

Step 6: Identify the Area of the Completed Square.

Given opposite sides are always equal, we can see that the missing piece is in fact a square.

The area of the missing square piece is $3^2 = 9$.

Given the big overall figure is a square (all side-lengths are $x+3$), then we have just completed the square!

So what is the area of the completed square? It is the original area $x^2 + 6x$ plus the area of the small missing square piece (9). So the total area is $x^2 + 6x + 9$.

Step 7: Factor the Perfect Square Trinomial

The number 9 in this case is a magic number, because now this creates a Perfect Square Trinomial. Trinomial means it’s an expression with 3 terms. Perfect Square because it can be factored to $(x+3)^2$ using the AC method. (If you forgot the AC method by the way, check out my YouTube video here.)

BUT GOOD NEWS! You don’t have to factor using the AC method anyway. Luckily there’s a nice beautiful shortcut.

The template is that it’ll always be $(x + \text{something})^2$. What is that “something”? Always half of b, which in this case was the number 6. Half of 6 is 3. (Note: $ax^2 + bx + c$)

Making Connections and Deriving the Complete the Square Method

Now that we’ve gone through the step-by-step derivation, let’s make some important connections and derive the complete the square formula.

Identifying the a, b, and c Values

In the standard form of a quadratic equation, $ax^2 + bx + c$, we can identify the values of a, b, and c in our example.
In the example $x^2 + 6x + 9$: a = 1, b = 6, and c = 9.

Cutting b in Half and Squaring the Result

Remember when we took the rectangle 6x and cut it in half? This created two 3x rectangles. Since b=6, to get to the number 3, we’ll divide by 2.

So the next step is to do $\frac{b}{2}$.

… and then the next thing we did was find the area of that little missing square piece, which was 9. How do we get from 3 to 9? By squaring 3!

So the step after doing $\frac{b}{2}$, is then squaring it. So $\left( \frac{b}{2} \right)^2$. This is the “magic number” that we’ll add to both sides.

Perfect Square Trinomial

By adding $\left( \frac{b}{2} \right)^2$ to both sides (remember that adding the same number to both sides doesn’t change the answer), now we have created a Perfect Square Trinomial.

Convert the Perfect Square Trinomial into Factored Form

The template here is $(x + \frac{b}{2})^2$.

Deriving the Complete the Square Steps

I go over a Complete the Square example in my video. Or you can read that in my blog post here.

Complete the Square Steps

Start with the standard form of the quadratic equation: $ax^2 + bx + c=0$
Make the leading coefficient a equal to 1 by dividing the entire equation by a. (Notice in the previous example $x^2 + 6x + 9$ we had a=1.)
Move the constant term c to the other side of the equation
Take half of the coefficient of the x term (b), square it, and add it to both sides of the equation
The resulting equation will be a perfect square trinomial, in which you use the template $(x + \frac{b}{2})^2$ to get it into factored form.
Finally, we can solve for x by using the Square-Root Method (taking the square root of both sides).

Solving by Quadratic Formula

Another method of solving quadratic equations is using the quadratic formula. We can also use the Complete the Square method to derive the Quadratic Formula. Check out that blog post or YouTube video or access that worksheet (with) key here!

Deriving Complete the Square Steps

First Things First

Related blog posts: