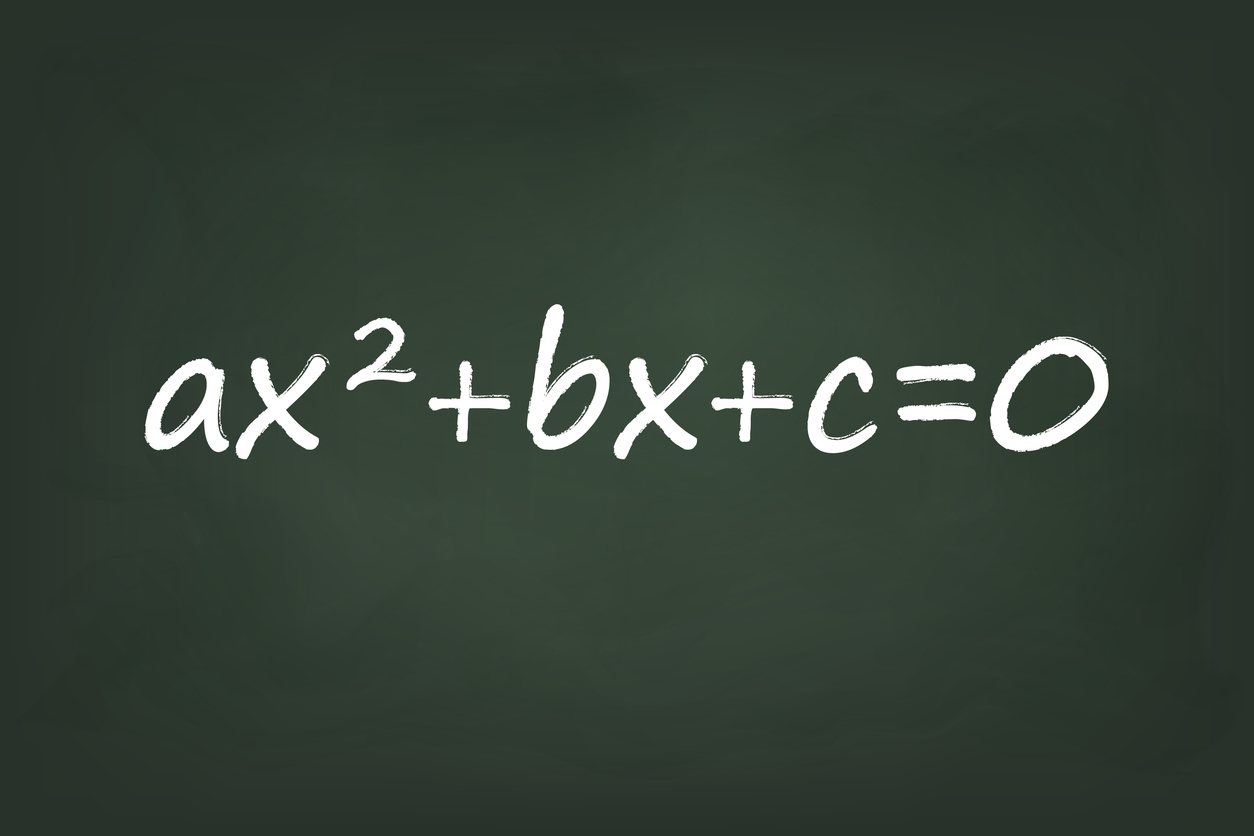In this blog post, we’ll dive into how to find the discriminant quadratic formula, and discover the relationship between the discriminant and real solutions. What is the discriminant formula in a quadratic equation? How do we use it? What does it mean to have a discriminant 0 vs. a positive discriminant vs. negative discriminant?
We’ll also look at 3 specific examples further down this blog post to find how the quadratic formula discriminant (the number underneath the radical sign in the quadratic formula) is connected to the nature of roots, and ultimately find how many x-intercepts the parabola has.
So if you forgot how to even use the quadratic formula, you might want to first read my Solve Quadratic Equations Example blog post, or watch my YouTube video about it.
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra FYI!
Take a look at my Quadratic Formula Derivation & Discriminant Activity worksheet with step-by-step keys.
Check out these related blog posts:
- Solve Quadratic Equations Example with a YouTube video about it.
- Quadratic Formula Derivation
- Complete the Square Examples
Foundation First
Before we look at how to find the discriminant of a quadratic equation, first we need to define:
- Real Number – Practically every number that you can think of on the number line (whole numbers, natural numbers, integers, rational and irrational numbers).
- Imaginary Number – The product of a real number and i, which is defined as $\sqrt{-1}$. Pretty much it’s the fact that your calculator gives you an “error” when you try to calculate a negative number under the square-root; that means it’s an imaginary number.
Quadratic Formula Discriminant
The discriminant formula is closely related to the quadratic formula.
- Quadratic Formula: $x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$
- Discriminant Formula: $b^2 – 4ac$
See a connection here? The discriminant is simply the number underneath the square-root symbol in the quadratic formula.
In a Nutshell – How To Use The Discriminant
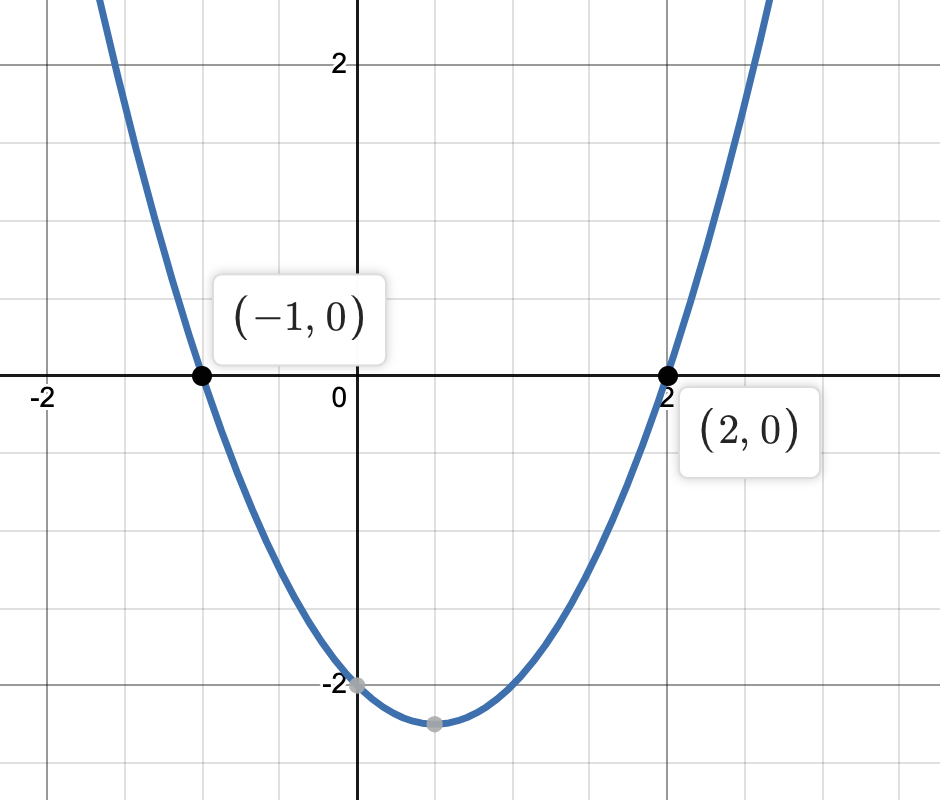
- Positive Discriminant produces 2 real solutions, which means that the parabola (“U” shape quadratic graph) will have 2 x-intercepts.
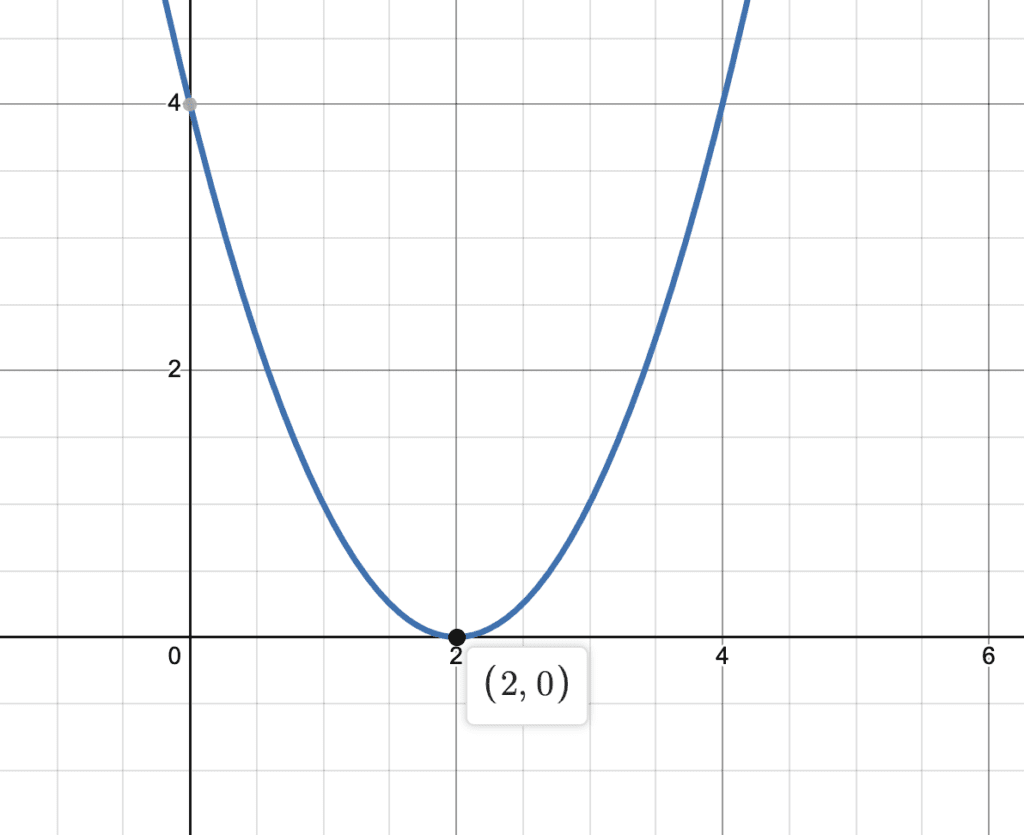
- Discriminant of 0 produces 1 real solution, which equates to 1 x-intercept.
- Negative Discriminant produces 0 real solutions (because they are 2 imaginary solutions; and so are not real), which equates to no x-intercepts at all.
Discriminant Practice Problems – Discovering Nature of Roots
How to find the discriminant of a quadratic equation? How to use the discriminant? Great questions! I thought you’d never ask.
You can find these problems and organized chart in my Quadratic Formula Derivation & Discriminant Activity worksheet with step-by-step keys.
Let’s get started!
Positive Discriminant
Let’s look at solving $2x^2 + 7x – 9 = 0$ using the quadratic formula: $\frac{-7 \pm \sqrt{(7)^2 – 4 \cdot 2 \cdot (-9)}}{2 \cdot 2}$. The discriminant remember is the number underneath the radical. So $(7)^2 – 4 \cdot 2 \cdot (-9)$ which equals 121. This is a positive number. Taking the square root of positive numbers always produces real results.
Let’s see what happens when we finish solving for x using the quadratic formula when we have a positive discriminant: $\frac{-7 \pm \sqrt{(7)^2 – 4 \cdot 2 \cdot (-9)}}{2 \cdot 2}$ = $\frac{-7 \pm \sqrt{121}}{4}$. Since the $\sqrt{121}$ is 11, and the $\pm$ symbol means there’s 2 scenarios (+11 and -11), then this quadratic equation produces 2 solutions and are therefore real numbers since the roots are 1 and -4.5. This would mean that the 2 x-intercepts would be at (1, 0) and (-4.5, 0) on your calculator. Remember that you can read my Solve Quadratic Equations Example blog post, or watch my YouTube video about it, if you can’t remember how to use the quadratic formula.
Discriminant of 0
For $x^2 + 4x + 4 = 0$, the quadratic formula produces: $\frac{-4 \pm \sqrt{(4)^2 – 4 \cdot 1 \cdot 4}}{2 \cdot 1}$. The discriminant is therefore $(4)^2 – 4 \cdot 1 \cdot 4$ which is equal to 0.
Since $\sqrt{0}$ = 0, what would the $\pm$ symbol in front of it imply? Well, +0 equals 0. And -0 is also 0. Therefore there’s actually only 1 case and that’s 1 real solution since 0 is a real number. This means the parabola only has 1 x-intercept. Where is the location of the x-intercept?
Finishing the quadratic formula we have : $\frac{-4 \pm \sqrt{0}}{2}$ which equals -2 only in either case. So (-2, 0) is the x-intercept here.
Negative Discriminant
For $x^2 – 5x + 11 = 0$, the quadratic formula produces: $\frac{5 \pm \sqrt{(-5)^2 – 4 \cdot 1 \cdot 11}}{2 \cdot 1}$. The discriminant is therefore $(-5)^2 – 4 \cdot 1 \cdot 11$ which equals -19.
Since $\sqrt{-19}$ is imaginary (it would give you an error on your calculator because it’s not real), then the $\pm$ symbol means there are 2 imaginary solutions. This is equivalent to saying 0 real solutions. And so graphically the parabola has no x-intercepts.
In Summary
Here is the answer key to my chart in my Quadratic Formula Derivation & Discriminant Activity worksheet: