In general, there are 3 formulas on how to factor a binomial [2 terms]: factoring the difference of 2 squares method (also known as the difference of perfect squares), the sum of cubes formula, and the difference of cubes formula. Feel free to check out my related blog on the Sum/Difference of Cubes method.
The difference of 2 squares is a special case of factoring a binomial, where it involves identifying two perfect squares and subtracting them. This is simply a template/formula that you follow to get the binomial into factored form. Let’s go over a few things followed by some examples.
The binomial does not have to be quadratic (degree or highest exponent is 2). We’ll go over some examples later where the degree is larger than 2.
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
Teachers can also access my lessons, keys, reference sheets for:
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
What is a Perfect Square?
A perfect square is a number or expression that can be represented as the product of a number multiplied by itself. For example, 4 is a perfect square because it can be written as $2 \times 2$, and $x^2$ is a perfect square because it can be written as $x \times x$.
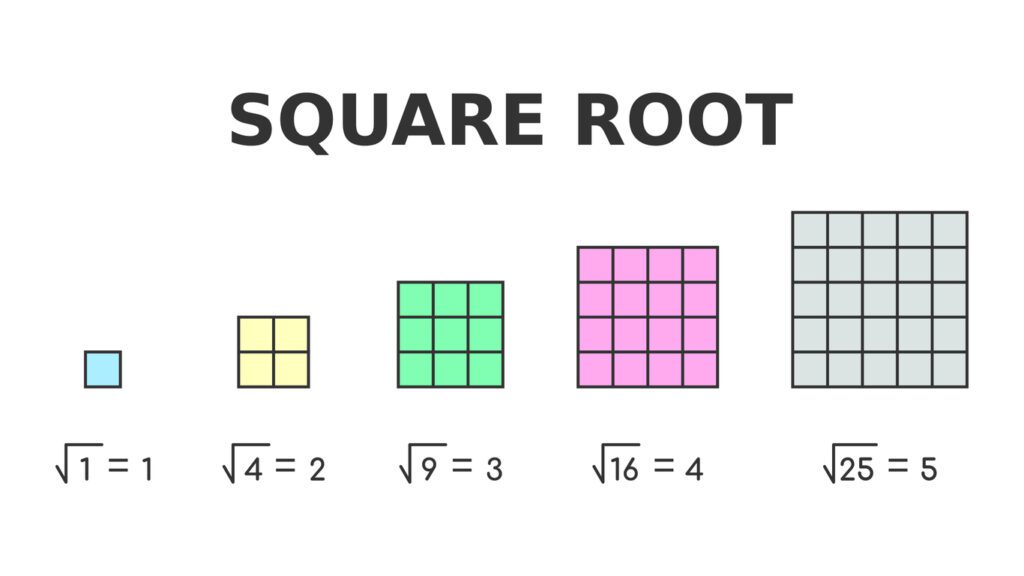
You can access the square-root symbol by the following ways:
- Raising the base to the one-half power (least common way).
- On a Ti-83/84 calculator, click the “2ND” button followed by the “$x^2$” button.
** If the exponent of the variable base is even, then it is a perfect square. This is because to find the square-root of the term, you simply divide the exponent by 2 (hence why it needs to be even). For example $x^8$ is a perfect square, since $\sqrt{x^8}=x^4$. Notice we cut the exponent 8 in half. We can do a check: $x^4 \times x^4$ is equal to $x^8$ because of the Product Rule.
The Difference of Perfect Squares Formula
The formula is: $a^2 – b^2 = (a + b)(a – b)$, where:
- a is the square root of the first term
- b is the square root of the second term
It’s important to understand that the order of the factors matters. The a term must come first, followed by the b term.
Below is a snapshot from my lesson slides with keys and notes:

Identifying Difference of Perfect Squares
The first step in factoring a polynomial using the difference of perfect squares formula is to identify whether the expression is indeed a subtraction of 2 perfect squares. Here are the key characteristics to look for:
- The polynomial must have two terms, connected by a subtraction sign.
- Each term must be a perfect square.
Examples:
Example 1: $x^2 – 9$
In this example, the first term, $x^2$, is a perfect square because it can be written as $x \cdot x$. The second term, 9, is also a perfect square because it can be written $3 \cdot 3$. Since the two terms are connected by a subtraction sign, this expression is a difference of perfect squares.
Example 2: $81 – 4x^2$
In this example, the first term, 81, is a perfect square because it can be written as $9 \cdot 9$. The second term, $4x^2$, is also a perfect square because it can be written as $2x \cdot 2x$. Since the two terms are connected by a subtraction sign, this expression is a difference of perfect squares.
Example 3: $x^4+9$
In this example, the first term, $x^4$, is a perfect square (since it’s equivalent to $x^2 \cdot x^2$), and the second term, 9, is a perfect square. But, the two terms are connected by an addition sign, not a subtraction sign. So don’t even think about using the formula! What this means is that it’s just not factorable. Period.
Factoring Examples
Once you’ve identified that an expression is a difference of perfect squares, you can use the formula to factor it. Here’s the step-by-step process:
- Identify the square root of the first term as a.
- Identify the square root of the second term as b.
- Substitute the values of
aandbinto the formula: $a^2 – b^2 = (a + b)(a – b)$.
Example 1: Factoring $x^2 – 9$
Step 1: Identify the square root of the first term, $x^2$, as $a = x$.
Step 2: Identify the square root of the second term, 9, as $b = 3$.
Step 3: Substitute the values of a and b into the formula: $x^2 – 9 = (x + 3)(x – 3)$
Example 2: Factoring $81 – 4x^2$
Step 1: Identify the square root of the first term, 81, as $a = 9$.
Step 2: Identify the square root of the second term, $4x^2$, as $b = 2x$.
Step 3: Substitute the values of a and b into the formula: $81 – 4x^2 = (9 + 2x)(9 – 2x)$
Checking Your Answer
After factoring the difference of perfect squares, you can check to see if it’s correct by simplifying that product. In other words, use the distributive property (or FOIL method). Then you can combine like terms or apply the commutative property of multiplication.
Example 1: Simplifying $(x + 3)(x – 3)$
This is equal to $x^2 + 3x – 3x – 9$. The middle like terms cancel out, and we get back the original $x^2 – 9$.
Example 2: Simplifying $(9 + 2x)(9 – 2x)$
This is equal to $81 – 18x + 18x – 4x^2$. The middle like terms cancel out, and we get back the original $81-4x^2$.
Factoring Completely
When factoring a polynomial, the final result doesn’t always have to be a product of 2 binomials. It can be a product of 3, and more.
Example: $x^4 – 16$
Step 1: Identify the square root of the first term, $x^4$, as $a = x^2$.
Step 2: Identify the square root of the second term, 16, as $b = 4$.
Step 3: Substitute the values of a and b into the formula: $x^4 – 16 = (x^2 + 4)(x^2 – 4)$
Notice that in the second parenthesis, $x^2 – 4$, can be factored again as the difference of two perfect squares, $x^2$ and 4. This is equal to $(x+2)(x-2)$.
Thus the full factored form of $x^4 – 16$ is $(x^2+4)(x+2)(x-2)$.
Polynomials with Different Variables
The difference of perfect squares method can also be applied to polynomials with variables, as long as the terms can be identified as perfect squares.
Example: Factoring $9w^2 – 4t^2$
Step 1: Identify the square root of the first term, $9w^2$, as $a = 3w$.
Step 2: Identify the square root of the second term, $4t^2$, as $b = 2t$.
Step 3: Substitute the values of a and b into the formula: $9w^2 – 4t^2 = (3w + 2t)(3w – 2t)$
Polynomials with Fractions
The difference of perfect squares method can also be applied to polynomials with fractional terms, as long as the terms can be identified as perfect squares.
Example: Factoring $\frac{1}{4}x^2 – \frac{1}{9}$
Step 1: Identify the square root of the first term, $\frac{1}{4}x^2$, as $a = \frac{1}{2}x$.
Step 2: Identify the square root of the second term, $\frac{1}{9}$, as $b = \frac{1}{3}$.
Step 3: Substitute the values of a and b into the formula:
$\frac{1}{4}x^2 – \frac{1}{9} = \left(\frac{1}{2}x + \frac{1}{3}\right)\left(\frac{1}{2}x – \frac{1}{3}\right)$