Remember first of all that a function is defined graphically as a relation that passes the vertical line test (has no repeating x-values). But the question is: Is the function even, odd or neither? What do these terms even mean by definition? And what does it mean graphically to be even or odd?
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
I also made a YouTube video about this, where I teach this lesson with full examples below step-by-step.
Even Functions
Graphically, an even function has symmetry about the y-axis, or a reflection over the y-axis. In other words, the left and right halves of the graph are mirror-images of each other, with the line of reflection being the y-axis (a.k.a. the vertical line $x=0$).
You will be asked algebraically to show that this is true using the following definition:
- A function $f(x)$ is considered an even function if it satisfies the condition $f(-x) = f(x)$ for all values of
xin the function’s domain. - What does $f(-x)$ even mean? It means that you substitute $(-x)$ into the x spot. If you forgot how to evaluate functions, you can check out my blog post on that here.
If that definition scares you, simply put, it means that when you plug $(-x)$ into the function, you get back the original function.
A Simple Example of an Even Function
Later, we’ll look at more complex functions. But for the sake of understanding the basics, here is a simple case:
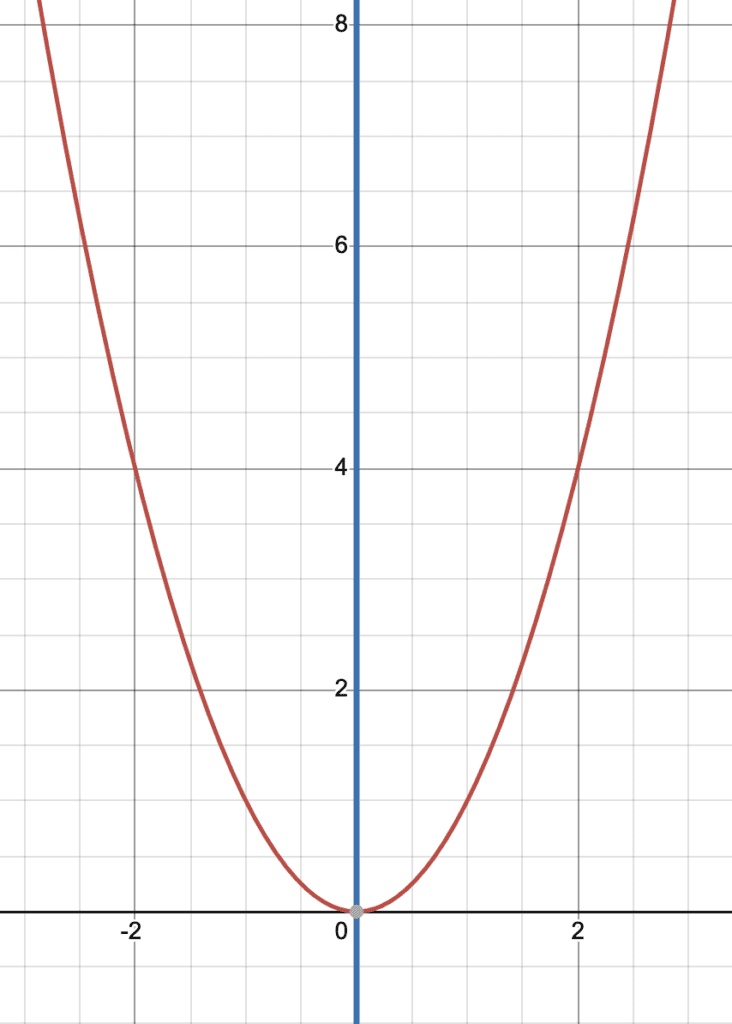
$f(x)=x^2$
Graphically: We can see visually that the line of reflection is the y-axis.
Algebraically:
To show that the function $f(x) = x^2$ is even, we need to verify that $f(-x) = f(x)$ for all x.
Here are the steps to show this:
- Find $f(-x)$. In other words, replace (x) with (-x) in the function $f(x) = x^2$.
So now we have $f(-x) = (-x)^2$. I can’t stress the importance of always substituting with parenthesis! - Simplify the expression:
So what is $(-x)^2$ simplified? This literally means $(-x) \cdot (-x)$, which is $x^2$ since a negative times a negative equals a positive.
So we just proved that $f(-x) = x^2$, which is the original function! Thus it’s even.
SHORTCUT: If a negative number is raised to an even power, then it always simplifies to a positive number. If a negative number is raised to an odd power, then it simplifies to a negative number.
More Challenging Even-Function Example
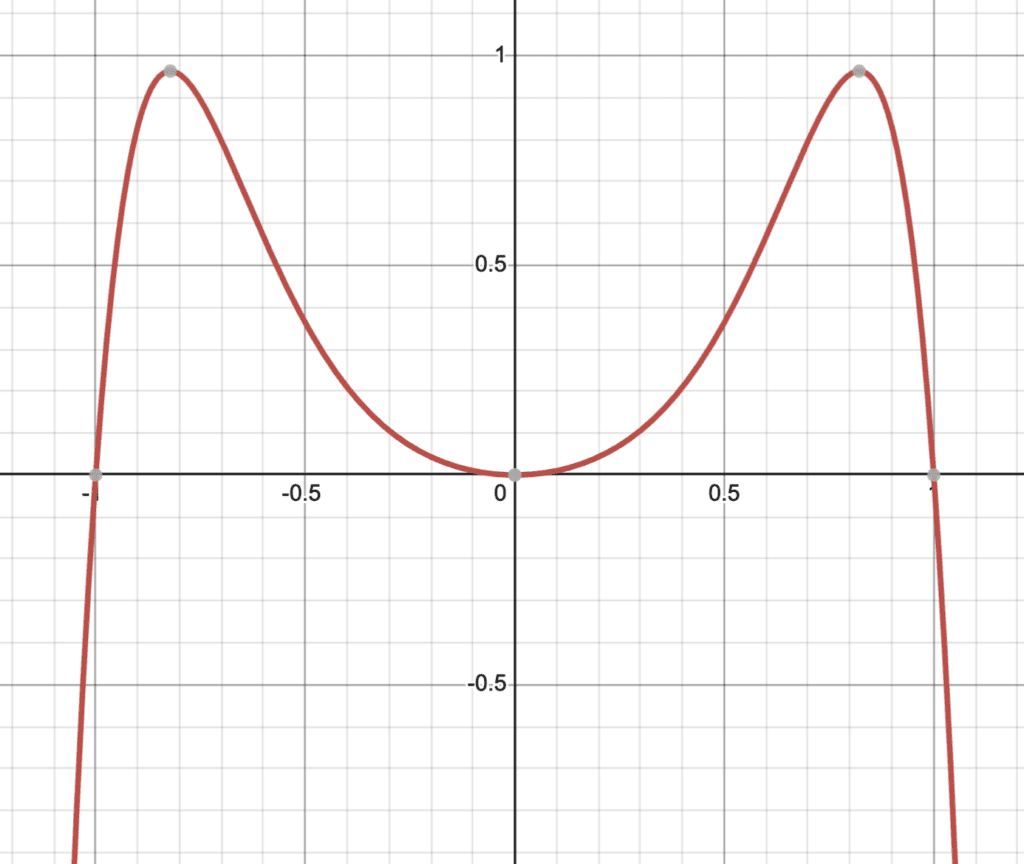
How about $x^2+2x^4-3x^8$.
Graphically, we can see that it is symmetrical over the y-axis:
I always first check if it is even since that is easier. We need to always start with finding $f(-x)$. So replacing x with (-x) we get: $f(-x)=(-x)^2+2(-x)^4-3(-x)^8$.
Then we simplify. Remember that anything raised to an even power will end up being positive. And anything raised to an odd power is negative.
Since all exponents are even, then all of the numbers inside the parenthesis turn into a positive.
So we have: $f(-x)=x^2+2x^4-3x^8$. This is actually the original function $f(x)$! Thus $f(-x)=f(x)$ and it is even.
Note: If you’re confused as to why the last term $-3(-x)^8$ turned into $-3x^8$, remember that the overall term should stay negative because a negative times a positive is still a negative.
Odd Functions
Graphically, an odd function has symmetry about the origin (0, 0). But what the heck does that even mean? It means that if you were to flip your paper upside down, it would still look like the same function.
Algebraically, this can be shown by the following definition:
- A function $f(x)$ is considered an odd function if it satisfies the condition $f(-x) = -f(x)$ for all values of
xin the function’s domain.
This means that the function changes signs when the input is negated.
Simple Example of an Odd Function
$f(x)=x^3$
Graphically: Try it! If you sketch this picture yourself, flip your paper upside-down and you’ll see that it looks exactly the same. This means there’s symmetry about the origin.
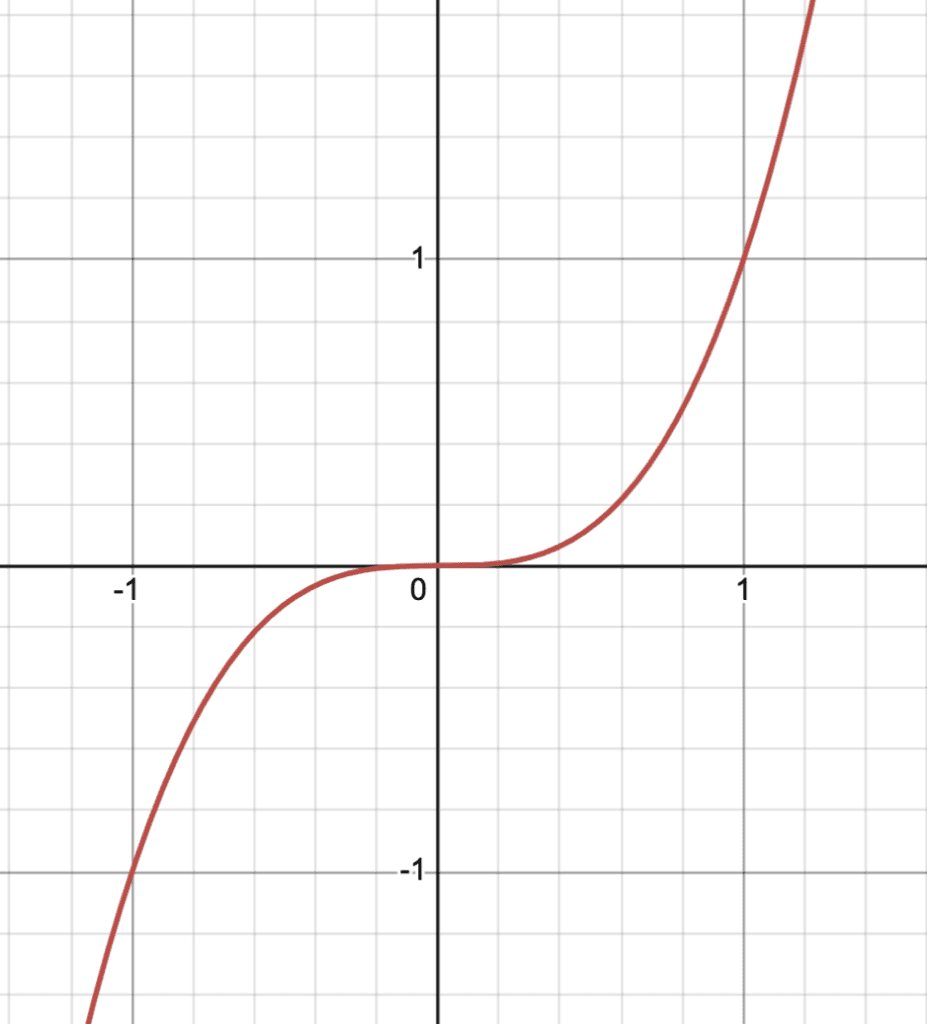
Algebraically:
To show that the function $f(x) = x^3$ is odd, we need to verify that $f(-x) = -f(x)$ for all x.
Here are the steps to show this:
- Find $f(-x)$. In other words, replace (x) with (-x) in the function $f(x) = x^3$.
So now we have $f(-x) = (-x)^3$. I can’t stress the importance of always substituting with parenthesis! - Simplify the expression:
So what is $(-x)^3$ simplified? This literally means $(-x) \cdot (-x) \cdot (-x)$, which equals $-x^3$ since a negative times itself 3 times equals a negative number.
Remember the shortcut that since it is raised to an odd power (3), then the answer is a negative number.
So we just proved that $f(-x) = -x^3$. Thus it’s odd.
Notice that the negative sign “came out” of the parenthesis. The more mathematical thing to say is that we’re left with the negation of the original function.
More Challenging Odd-Function Example
Let’s consider $f(x) = x^5 + 3x^3$.
Graphically, we can see that this is symmetrical about the origin (if you flip the paper upside-down, it looks exactly the same).
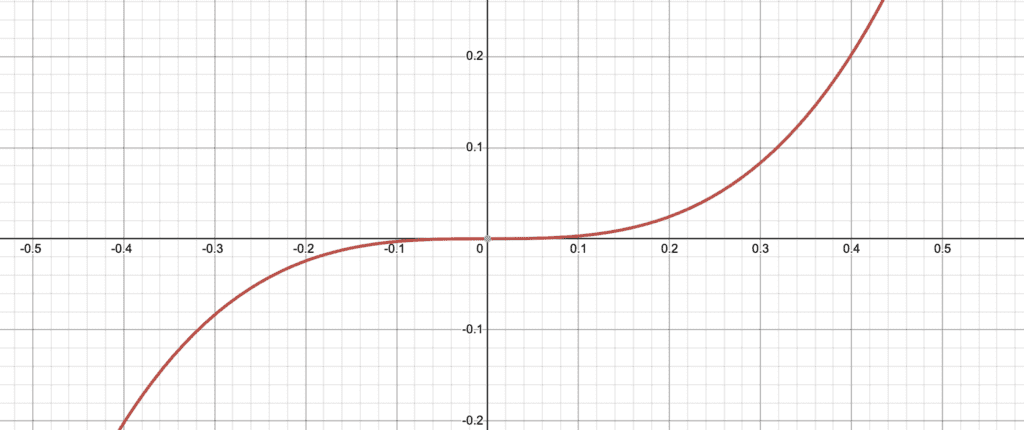
Algebraically we’ll do the following steps:
Step 1: Substitute (-x) into the function: $f(-x) = (-x)^5 + 3(-x)^3$.
Step 2: Simplify the expression.
Remember the shortcut: If a negative number is raised to an even power, then it always simplifies to a positive number. If a negative number is raised to an odd power, then it simplifies to a negative number.
Since both exponents are odd numbers, then both terms stay negative: $f(-x) = -x^5 – 3x^3$.
Step 3: Analyze the result.
First we check if it’s even. For it to be even, $f(-x)$ must be equal to the original function $f(x) = x^5 + 3x^3$. Is it? No! $f(-x) = -x^5 – 3x^3$ is not the same as $f(x) = x^5 + 3x^3$. So it’s not even.
Now we’ll check if it’s odd. For it to be odd, $f(-x)$ must be equal to $-f(x)$.
Here’s the simple way of checking that this is true: If all of the terms are opposite signs of the original function, then it’s odd.
Comparing $f(-x) = -x^5 – 3x^3$ and the original $f(x) = x^5 + 3x^3$, we can see that both terms are opposite signs (they both turn positive).
Since $f(-x) = -f(x)$, then the function $f(x) = x^5 + 3x^3$ is odd.
Neither Even Nor Odd
If a function does not meet either algebraic condition, then it’s neither. Simple as that.
And graphically, the function does not show any symmetry properties about the y-axis or the origin.
Example: $f(x)=1+x+x^2$.

Graphically, we can see that the y-axis does not split the graph into 2 halves. So it can’t be even. And if you flip your paper upside-down, it won’t look exactly the same (meaning it’s not symmetrical about the origin). So it can’t be odd.
Algebraically, let’s see why this is true:
First we’ll check if it’s even: $f(-x)=1+(-x)+(-x)^2$. The middle term has an odd exponent (1), and the last term has an even exponent (2). So we’ll keep the middle term negative, and turn the last term into a positive.
(Remember the shortcut: Anything raised to an even power is positive, and anything raised to an odd power is negative.)
So after simplifying we have: $f(-x)=1-x+x^2$. Is this the same as the original function? No. So it’s not even.
Next, we’ll see if it’s odd. The simple way of looking at it is that if all of the terms are opposite signs of the original function, then it’s odd.
To check this, we ask ourselves: Do all the terms in $f(-x)=1-x+x^2$ have opposite signs as the original function $f(x)=1+x+x^2$?
No. So it’s not odd either. Therefore the function is neither even or odd.
Compare/Contrast Even and Odd Functions
Similarities:
- To prove whether a function is even, odd or neither, the starting point is always the same: Find $f(-x)$, which means to replace x with $(-x)$.
- Graphically, they both have symmetries.
Differences:
- If after finding $f(-x)$, you get back the original function $f(x)$, then it’s even.
- If after finding $f(-x)$ and you notice that all of the signs of each term change, then this means it is equal to $-f(x)$, and therefore is odd.
- Even functions are symmetrical over the y-axis. Odd functions are symmetrical about the origin.
In a nutshell:
- If $f(-x) = f(x)$, then the function is even.
- If $f(-x) = -f(x)$, then the function is odd.
- If $f(-x)$ does not equal $f(x)$ or $-f(x)$, then the function is neither even nor odd.
Practical Applications of Even and Odd Functions
Understanding the properties of even and odd functions can be useful in various areas of mathematics and science. Here are a few examples of their practical applications:
Trigonometric Functions
Many trigonometric functions, such as sine and cosine, are either even or odd functions. For instance, the sine function is an odd function, while the cosine function is an even function. This knowledge can simplify the analysis and manipulation of trigonometric expressions.
Electrical Engineering
In electrical engineering, even and odd functions are used to analyze the behavior of electrical circuits and signals. For example, even functions are often used to represent the voltage-current characteristics of certain electronic components, while odd functions are used to model the behavior of amplifiers and other nonlinear devices.
Quantum Mechanics
In quantum mechanics, the wave functions of particles can be classified as even or odd functions, depending on the symmetry properties of the system. This classification is crucial for understanding the behavior of quantum systems and the properties of subatomic particles.