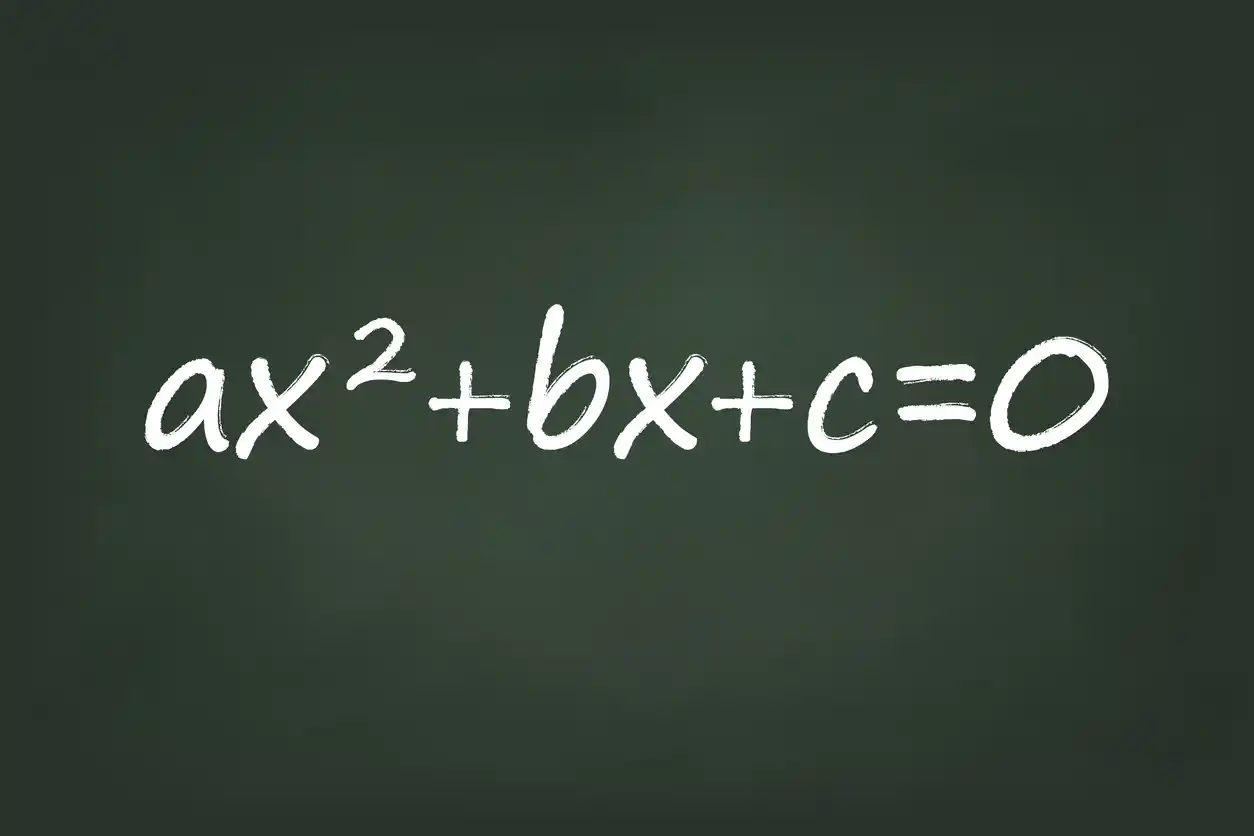In this blog post we’ll talk about the Power Rule for exponents. We’ll also go over Product, Quotient, Zero-Exponent and Negative-Exponent Rules in depth. Towards the bottom of this blog post we’ll go over some examples. Understanding the properties of exponents is crucial for simplifying and manipulating functions.
First Things First
If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.
You can also access my Properties of Exponents – 77 Problems & Reference Sheet with Keys.
If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!
If it’s easier for you as a more visual learner, check out my YouTube video where I go over all properties of exponents as well as foundational concepts that students often confuse.
Foundation
Before we dive into the properties of exponents, let’s quickly review the basics.

In a nutshell, an exponent represents repeated multiplication of a base number. For example, in the expression $x^4$, the base is x, and the exponent is 4, which means that x is multiplied by itself four times: $x \cdot x \cdot x \cdot x$.
Exponents can be positive, negative, or even fractions, and they play an important role in many operations and functions, like exponential growth and decay, logarithms, and power functions.

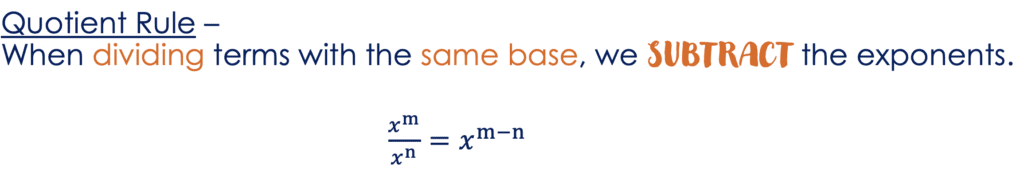
Product Rule
The product rule states that when you multiply two expressions with the same base, you add the exponents. In general: $x^m \cdot x^n = x^{m+n}$
For example, if we have $x^2 \cdot x^3$, remember that since $x^2 = x \times x$ and $x^3 = x \times x \times x$, then $x^2 \cdot x^3 = x \cdot x \cdot x \cdot x \cdot x$. And so this equals $x^5$.
As a shortcut method, we can apply the Product Rule to simplify it as $x^{2+3} = x^5$.
Power Rule
The power rule states that when you raise a power to another power, you multiply the exponents. In general:
$(x^m)^n = x^{m \cdot n}$
For example, if we have $(x^4)^3 $ since the entire base is $x^4$ and it’s raised to the third power, that means we should be multiplying $x^4$ times itself 3 times. So that’s $x^4 \cdot x^4 \cdot x^4$. Now we can apply the Product Rule to then add the exponents: $x^{4+4+4} = x^{12}$
As a shortcut, using the Power Rule we can simply multiply the exponents: $x^{4 \times 3} = x^{12}$.
Quotient Rule
The quotient rule states that when you divide two expressions with the same base, you subtract the exponents. In general: $\frac{x^m}{x^n} = x^{m-n}$
For example, if we have $\frac{x^5}{x^2}$, that’s saying $\frac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x}$. Two of the $x$’s cancel out, and so we’re then left with three $x$’s, or $x^3$.
We can simply apply the Quotient Rule to simplify it as $x^{5-2} = x^3$.
Zero Exponent Rule
The zero exponent rule states that any base (other than zero) raised to the power of zero is equal to 1. Mathematically, for any non-zero base x, the following equation holds: $x^0 = 1$, regardless of the value of x.
How Can This Be?
Well, suppose we have something like $\frac{x^m}{x^m}$. We all know that anything divided by itself is 1. So $\frac{x^m}{x^m}$ = 1.
Okay, now let’s go back to $\frac{x^m}{x^m}$ and use the Quotient Rule, that’s $x^{m-m}$. Since $m-m = 0$, then we have $\frac{x^m}{x^m} = x^0$.
Okay! So now we just proved 2 things:
- $\frac{x^m}{x^m}$ = 1
- $\frac{x^m}{x^m} = x^0$
By the transitive property, since 1 and $x^0$ are both equal to $\frac{x^m}{x^m}$, then they must both be equal to each other.
So $x^0 = 1$ 😃
Negative Exponent Rule
The negative exponent rule states that any base raised to a negative exponent is equal to the reciprocal of the base raised to the positive exponent. In general: $x^{-m} = \frac{1}{x^m}$
Huh?
Okay, so all you do is take the base with the negative exponent, and then “move” it to the other side of the fraction. In other words, if that base was at the top, now it moves to the bottom, and vice versa.
… And in the process of moving, then that exponent turns positive.
For example, $x^{-3}$ is also saying $\frac{x^{-3}}{1}$. So $x^{-3}$ is at the top of the fraction. That means it would move to the bottom (and then the exponent turns positive). So $x^{-3} = \frac{1}{x^3}$.
A crazier example is $\frac{x^2 y^{-4}}{z^{-2} t^8}$. The only bases with negative exponents are $y$ and $z$. So those are the only ones that are moving, and again the exponent turns positive after they move. So that’s equal to $\frac{x^2 z^2}{y^4 t^8}$.
Combining Like Terms
I do need to strain the importance that in this blog, we have not talked about adding or subtracting bases. For example: $x^4 + x^2$. These are not what’s called “like-terms”. And so this is as simple as we can get; there is nothing we can do.
However if it was multiplication, then we’d use the Power Rule: $x^4 \times x^2 = x^{4+2} = x^6$.
Anyway, when adding or subtracting bases, in order for them to be “like-terms”, they must both have the same base and must have matching exponents. When this is the case, then we would add or subtract the coefficients. So let’s say we have $2x^2 + 6x^2$. That would be equal to $8x^2$.
Notice that the exponent does not change here. The only times when the exponents change is when we use the rules learned in this blog.
Happy Learning!