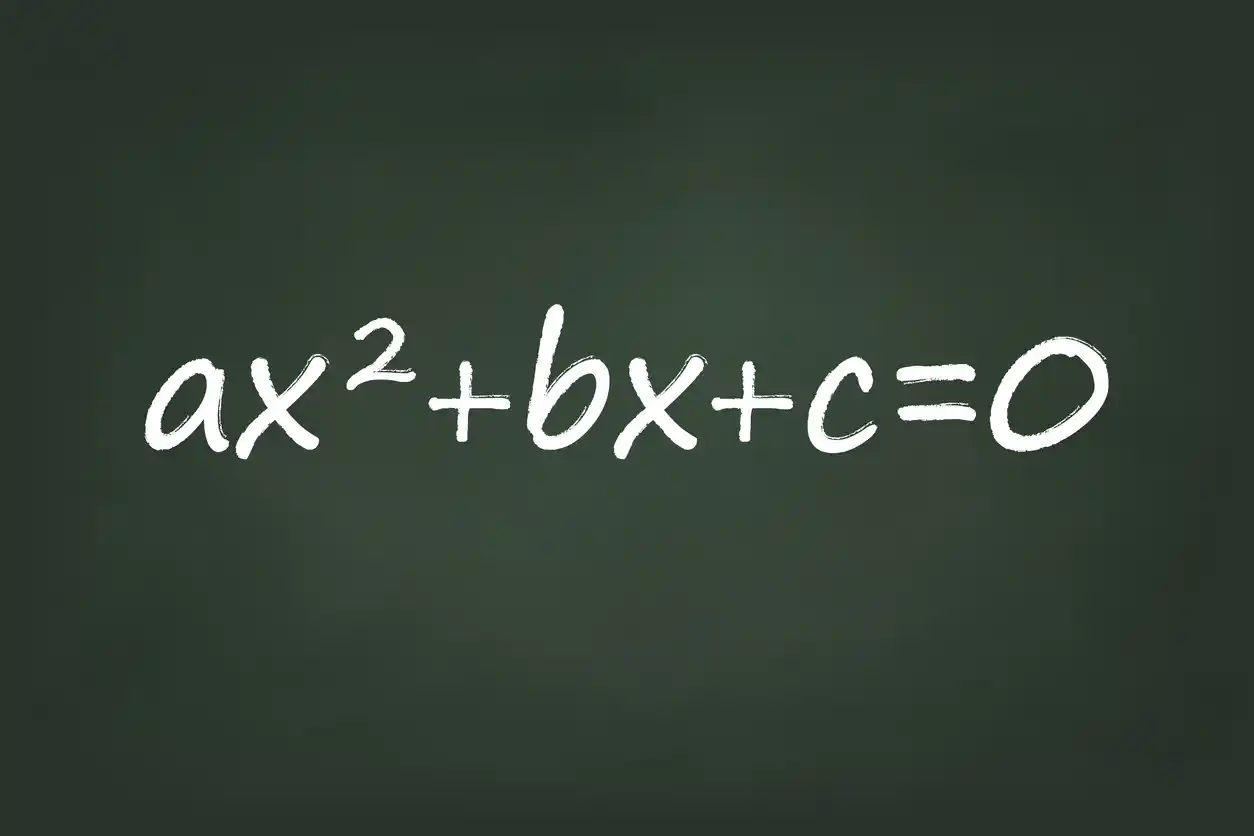Quadratic Formula Derivation

Hey Friend! You can skip straight to the Quadratic Formula derivation down below. Otherwise, I’d like to first highlight very important Warm Up skills needed for the quadratic formula proof through Completing the Square. If you’d like the worksheet (with keys) that I used for this lesson, grab them here!

If you, first of all, forgot the Completing the Square steps, then you can read my blog post here to review. Or, I made a video about using the Complete the Square method here.

And if you’re more of a visual person, I made a video from everything that I talk about in this blog post (using the same worksheet) on deriving the quadratic formula. Take a look below!

First Things First

Related Blog Posts:

• Quadratic Formula Discriminant
• Quadratic Formula Example with a YouTube video about it
• Complete the Square Examples
• Deriving the Complete the Square Method – YouTube Video

If you’re a teacher reading this, did you grab my *FREE* Algebra 2 Pretest (10 pages) with answers yet? Click here.

Also my How To Teach the Quadratic Formula post here.

If you’re a student, this topic is also one of my modules in my online course to get a solid foundation in any high school math subject, not just in Algebra 2 FYI!

Skill Review – Foundation First!

Anyway! The quadratic formula derivation needs Warm Up skills so that it’s easier to understand it during the proof. You can access my entire worksheet with key here if you prefer everything written below in an organized page.

See if you can get these right on your own first:

1. $\frac{4}{5} \div 2$
2. $\left( \frac{3}{4} \right)^2$
3. $\frac{3}{8} + \frac{1}{4}$
4. $\sqrt{\frac{3}{25}}$
5. Is $-c \times 4a$ the same as $-4ac$?
6. Use the commutative property of addition to write the equivalent expression for: $-4ac + b^2$

The solutions are:

1. Keep change flip! $\frac{4}{5} \times \frac{1}{2}$ which equals $\frac{4}{10}$ = $\frac{2}{5}$
2. When you have a fraction raised to a power, you can “distribute” the exponent to both the numerator and denominator: $\frac{3^2}{4^2}$ = $\frac{9}{16}$
3. When adding (or subtracting) fractions, we need a common denominator. The LCD (least common denominator) is 8. And so we need to multiply the top and bottom of $\frac{1}{4}$ by 2 because 4 times 2 is 8. In doing so, the new expression is $\frac{3}{8} + \frac{2}{8}$ which equals $\frac{5}{8}$ as we combine the numerators.
4. Similar to squaring a fraction (like problem #2), the same goes for square-rooting where we will “distribute” that operation. So that’s $\frac{\sqrt{3}}{\sqrt{25}}$. And since 25 is a perfect square, the final answer is $\frac{\sqrt{3}}{5}$.
5. Yes they are the same because of the commutative property of multiplication.
6. The equivalent expression is $b^2 + (-4ac)$, which is also equal to $b^2 – 4ac$

Now that we got those skills out of the way, let the Quadratic Formula derivation begin!

The whole point of deriving the quadratic formula in the first place is so that we can reuse the formula over-and-over for solving quadratic equations in standard form: $ax^2 + bx + c = 0$. If you’ve ever wondered how the quadratic formula was derived, here are the complete steps below:

1. To Complete the Square, remember that the first step is always to make sure the leading coefficient (of the $x^2$ term) is 1. And so we must divide everything by a: $x^2 + \frac{b}{a}x + \frac{c}{a} = 0$
2. Next to complete the square, we always move the constant term to the other side of the equation. $x^2 + \frac{b}{a}x = -\frac{c}{a}$.
3. Now it’s time to add a specific number to both sides of the equation. Remember, as long as you’re adding the same number to both sides, you’ll never change the value of the solution. This is a theorem in math. What is it that we’ll be adding exactly?
4. Well, the number we add to both sides is to then take the coefficient of the middle term, in this case $\frac{b}{a}$ … we’ll cut this in half and then square it. This is is similar to Warm Up problem #1 from earlier in the blog. Let’s divide by 2: $\frac{\frac{b}{a}}{2}$. We need to keep, change, flip! And so we get $\frac{b}{2a}$. Now to square it, this is similar to Warm Up problem #2. Remember that we can “distribute” the exponent to top and bottom. And so the number that we are adding to both sides of the equation is $\frac{b^2}{4a^2}$.
5. So now in the Quadratic Formula Derivation process, we have what looks like: $x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} = -\frac{c}{a} + \frac{b^2}{4a^2}$.
6. The left-hand side of the equation is now called a Perfect Square Trinomial. The template is always “x plus something squared”. What is that “something”? It’s always half of the coefficient of the middle term. In this case $\frac{b}{2a}$.
7. So now we’re at: $(x + \frac{b}{2a})^2$ = $-\frac{c}{a} + \frac{b^2}{4a^2}$
8. The right-side of the equation, we need to simplify this. You can refer to Warm Up problem #3, where we need to get common denominators since we’re adding fractions. The LCD is $4a^2$. And so we need to multiply the first fraction (both top and bottom of course) by $4a$ in order to accomplish this. In doing so, that first fraction is now transformed to $\frac{-4ac}{4a^2}$. Note: Remember the commutative property of multiplication (Warm Up problem #5) that we want $-4ac$ in that specific order. Does it look familiar yet?
9. Now that they have common denominators, what’s next is to combine the numerators. And so adding those fractions we have $-4ac + b^2$. Lastly we’ll refer back to Warm Up problem #6 that is the exact problem. (Coincidence? I think not!). Because of the commutative property of addition, we can rearrange those as $\frac{b^2 – 4ac}{4a^2}$.
10. So now we have: $x + \frac{b}{2a} = \frac{b^2 – 4ac}{4a^2}$.
11. Let’s take the square-root of both sides because it is the opposite of squaring. Don’t forget to always put the $\pm$ symbol every time we take the square-root when solving for x! So now we have, like Warm Up problem #4, $\frac{\sqrt{b^2 – 4ac}}{\sqrt{4a^2}}$ . Since $4a^2$ is a perfect square, it equals 2a. So now we have $x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 – 4ac}}{2a}$.
12. We are ONE MORE STEP away in deriving the quadratic formula steps! What is stopping x from being by itself? It is being added by $\frac{b}{2a}$. So we need to subtract it: $x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 – 4ac}}{2a}$
13. Given they already have a common denominator, we can finally combine those fractions to finally produce the quadratic formula: $x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$

Congratulations! The quadratic formula derivation proof is finally complete. Great job for following along and sticking to the end!