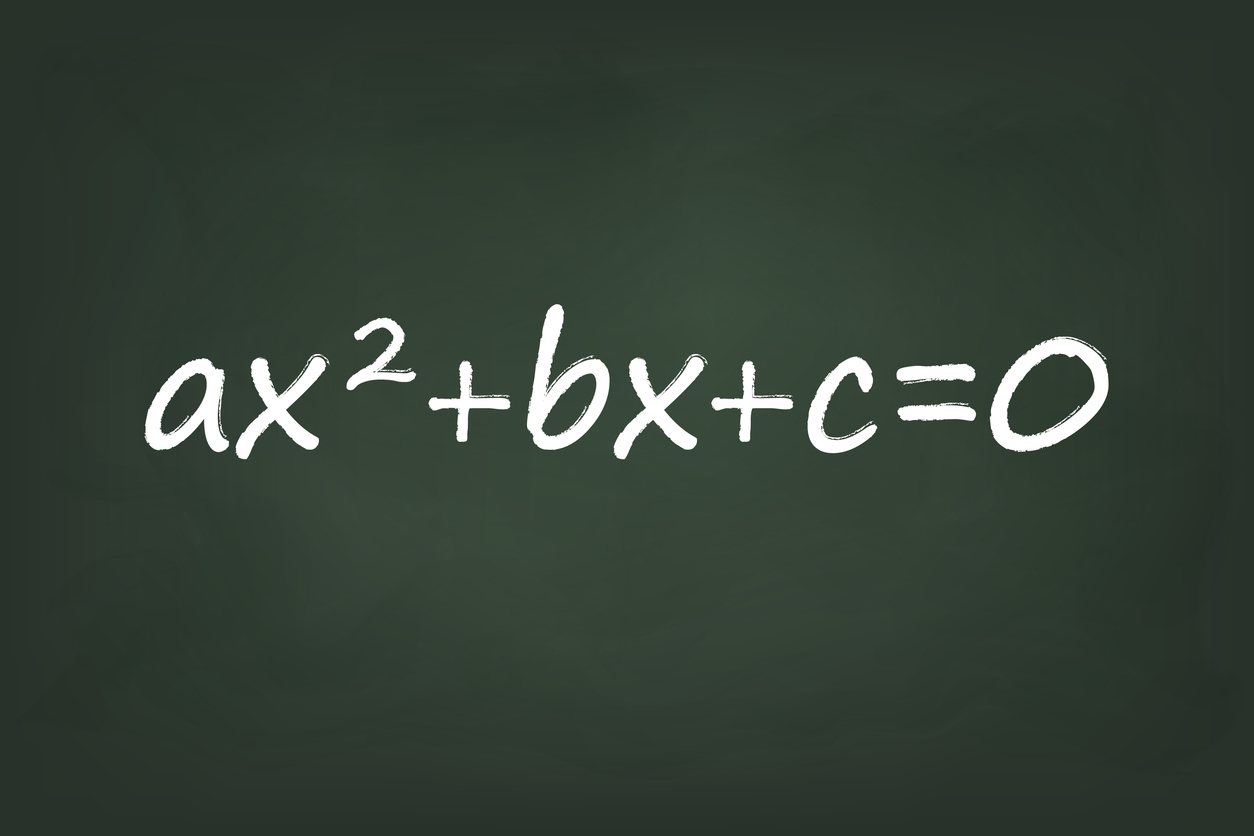The quadratic formula in standard form $ax^2 + bx + c = 0$ is $x = \frac{{-b \pm \sqrt{{b^2 – 4ac}}}}{{2a}}$. There are many ways in solving quadratic equations. This blog post focuses on how to effectively teach the quadratic formula steps to solve for the roots.
First Things First
Did you download yet my *FREE* research-based Algebra 2 Pretest with Answers here?
Check out my related lesson on how to Derive the Compete the Square steps in my YouTube video here. And you can access these worksheets with keys here.
Anyway, you can head over to my student blog if you forgot the math content on the quadratic formula, where I go over the steps more in depth with an example. Or, you can check out my YouTube video here as I visually go over an example on solving using the quadratic formula where you must first convert to standard form. And I also visually show the quadratic formula in ti-84 steps.
Prerequisites
Before teaching the quadratic formula steps, we need to make sure that students are familiar with the concepts:
- Students knowing what a quadratic function even is. It’s where the degree (highest exponent) is 2. I can’t tell you how many times I see people attempt to use the quadratic formula where the degree is not 2. I’m sure you’ve seen this too!
- Understanding quadratic equations and their forms (standard form $ax^2 + bx + c = 0$, vertex form $y = a(x – h)^2 + k$, and factored form $y = a(x – r_1)(x – r_2)$ where r is a root).
- Knowledge of solving linear equations and basic algebraic manipulations.
- Familiarity with square roots, simplifying radicals, and simplifying fractions.
Step-by-Step Guide
1. Warm Up:
- Give a Warm Up on simplifying radicals and simplifying rational expressions. That way, I find it’s not as overwhelming later when students see, what may feel like to them, a whole bunch of numbers, symbols, parenthesis and roots all squished together. And what the heck is that plus/minus symbol!? Scary to them. Scaffolding is always key.
2. Motivation for the Quadratic Formula:
- I can’t tell you how many students don’t understand why they are even using the quadratic formula. Ultimately it’s to find the roots, which we’ll talk more about the discriminant later.
- …. But the other main connection is … when do we even use it? You can begin the lesson with an example where students try to solve a quadratic equation by factoring (check out that lesson with key here), but it’s not factorable! This is THE perfect time to emphasize there’s a dire need to an alternative method. Some of the steps of my derivation worksheet are down below:
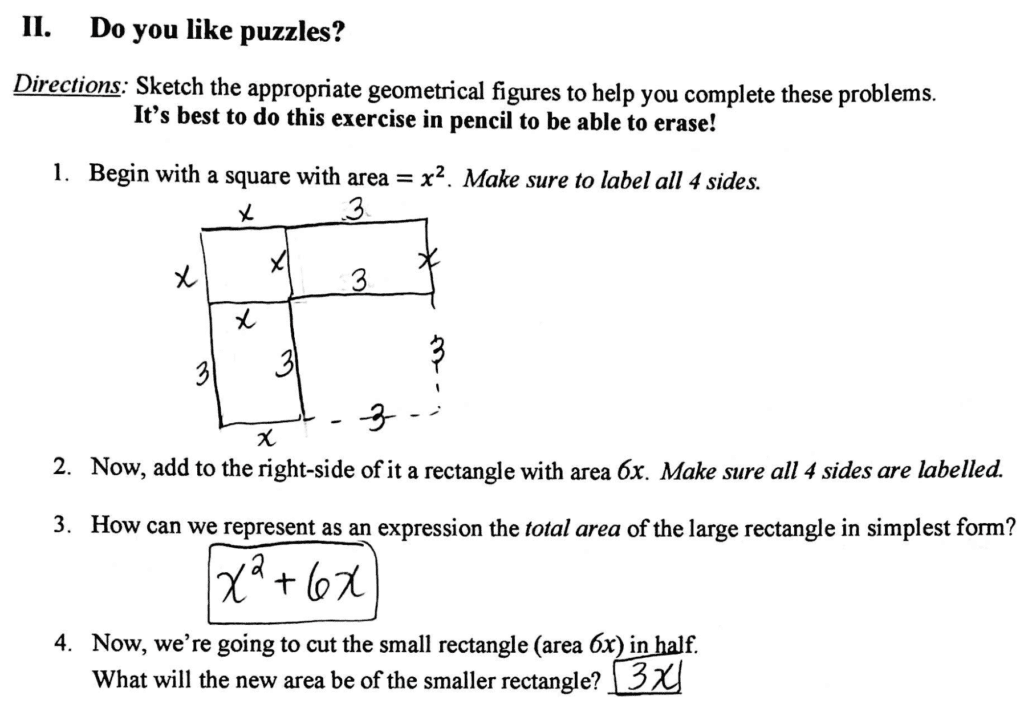
- Also use this time to tell students that if a quadratic equation is not factorable, the only 2 other options are the quadratic formula and completing the square. Feel free to check out my worksheet & key on the deriving the Complete the Square method here.
3. Derivation of the Quadratic Formula:
- If your [insanely] busy curriculum allows for time, it would be an excellent idea for students to see where the quadratic formula actually comes from. I created this quadratic formula derivation here (with key) that guides students step by step on using the Complete the Square method to do this.
- Make sure to make the connection that the quadratic formula is simply the Complete the Square method already done for you!

4. The Quadratic Formula:
- I like to keep the quadratic formula: $x = \frac{{-b \pm \sqrt{{b^2 – 4ac}}}}{{2a}}$ written on the board. If students have a hard time remembering the quadratic formula, I like to use the “Pop Goes the Weasel” version that I know it helps me remember to this day. My teacher thankfully taught it to me when I was in high school. Never heard of it? Click here to listen.
- Explain the meaning of each component a, b, and c, and how they relate to the coefficients in the standard form equation. I always tell students that sometimes (us teachers) can be sneaky and rearrange the terms to no longer be in standard form. In that case, they must surely remember that a is the coefficient of the $x^2$ term, b is the coefficient of the x, and c is called the constant with no x attached to it.
- I find it successful to have students always set themselves up with: a=___ b=____ c=____. I personally give some partial credit if they at least have identified them correctly.
5. Practice and Application:
- Walk through examples of using the quadratic formula in standard form to solve quadratic equations.
- I like to start with a simple example and gradually increase the complexity to ensure understanding.
- Emphasize checking solutions by substitution back into the original equation.
- I also like to solve the same equation by factoring to literally show students you get the same answer, and that it works (we’re not just pulling things out of thin air, like it may sometimes seem to students whose minds get blown everyday!).
- Include a variety of problems, including real-world applications and contextual problems.
- Encourage students to discuss their approaches and strategies for solving each problem.
6. Next Class:
- The next class should most definitely be a discovery-style approach where students solve for 3 equations for the following discriminant values: negative, zero, and positive.
- Instead of students just being spoon-fed this information, it really goes a long way when students actually see why a negative discriminate produces no real roots, and so there would not be any x-intercepts on the graph. Then you can even have them graph it on the calculator or use Desmos to have it confirmed.
- The same goes for the fact that a zero discriminant produces 1 real solution and so 1 x-intercept (because the square root of zero is zero; only one answer is possible); as well as a positive discriminant produces 2 real solutions and so there are 2 x-intercepts.
7. Common Mistakes and Pitfalls:
- Highlight common mistakes students make when applying the quadratic formula (e.g., sign errors, misidentifying coefficients). In my student blog post here, scroll towards the bottom where I go over all the common mistakes.
- Provide strategies for avoiding these mistakes and emphasize the importance of accuracy in calculations.
8. Assessment:
- As always (or else teachers get in trouble 😂) assess student understanding through quizzes, tests, or problem-solving tasks that require the use of the quadratic formula in standard form.
- Provide constructive feedback and additional support for students who need it.
9. Resources and Tools:
- Utilize technology tools, such as graphing calculators or online resources, to visualize quadratic equations and solutions.
- Recommend resources like textbooks, worksheets, and online tutorials (or my online courses 😃) to support independent learning.